Chứng minh biểu thức N=2x2 + 7y2 - 6xy + 10x - 30y +45
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
15 tháng 4 2019
\(N=2\left(x^2+\frac{9y^2}{4}-3xy+5x+\frac{25}{4}-\frac{15}{2}y\right)+\frac{5}{2}\left(y^2-6y+9\right)+10\)
\(N=\left(x-\frac{3}{2}y+\frac{5}{2}\right)^2+\frac{5}{2}\left(y-3\right)^2+10>0\) \(\forall x;y\)
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 6 2019
a/
\(\Leftrightarrow x^2-2xy+y^2+2x^2+10x+26=0\)
\(\Leftrightarrow\left(x-y\right)^2+2\left(x-\frac{5}{2}\right)^2+\frac{27}{2}=0\)
\(VT>0\Rightarrow\) ko tồn tại x; y thỏa mãn
b/
\(\Leftrightarrow4x^2-4x+1+3\left(y^2+10y+25\right)+2=0\)
\(\Leftrightarrow\left(2x-1\right)^2+3\left(y+5\right)^2+2=0\)
\(\Rightarrow\) Không tồn tại x; y thỏa mãn
c/
\(3\left(x^2-4x+4\right)+6\left(y^2-\frac{10}{3}y+\frac{25}{9}\right)+\frac{34}{3}=0\)
\(\Leftrightarrow3\left(x-2\right)+6\left(y-\frac{5}{3}\right)^2+\frac{34}{3}=0\)
Không tồn tại x; y thỏa mãn
CM
8 tháng 3 2019
Với x = 20040, ta có: A = 10/20040 = 1/2004.
Vậy A = 1/2004 khi x = 20040.
CM
1 tháng 7 2017
Với x = 20040, ta có: A = 10/20040 = 1/2004.
Vậy A = 1/2004 khi x = 20040.
LH
2 tháng 6 2018
a) A= \(\left(x^2-2xy+y^2\right)+\left(x^2+10x+25\right)+x^2+1\)1
=\(\left(x-y\right)^2+\left(x+5\right)^2+x^2+1\ge1\)
\(\Rightarrow\)A dương với mọi x,y
CM
16 tháng 12 2019
Giá trị của biểu thức xác định khi mỗi giá trị của phân thức trong biểu thức đều được xác định.
Khi đó điều kiện xác định:
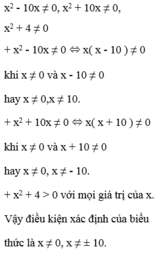
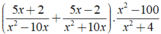
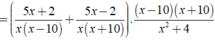
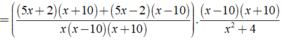
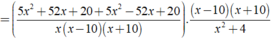
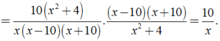
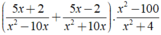
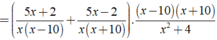
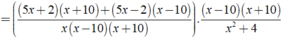
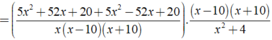
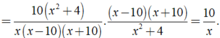
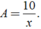
CM j z bn???
Chứng minh N luôn nhận giá trị dương với mọi x,y. (sorry, mình gõ thiếu)