hãy nêu hai cách giải cho bất phương trình sau :
\(|2x-4|=6\)
nhanh hộ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1, \(3x+4< 0\Rightarrow3x< -4\)\(\Rightarrow x< -\frac{4}{3}\)
2, \(2x-3>0\Rightarrow2x>3\)\(\Rightarrow x>\frac{3}{2}\)
3, \(1,2x< -6\Rightarrow x< \frac{-6}{1,2}\Rightarrow x< \)\(-5\)
4, \(3x+4>2x+3\)\(\Rightarrow3x-2x>3-4\)\(\Rightarrow x>-1\)
Đây là dạng cơ bản nhất của dạng giải bất phương trình nên nắm vững nhé
Chuyển vế, đổi dấu như thường, chỉ có nhân(chia) cho số âm thì đổi chiều thôi
chúc bạn học tốt nhé

<=> (10x+8)/12-(2x-1)/12>48/12
<=>10x+8-2x+1>48
<=> 10x-2x>48-8-1
<=>8x>39
<=> x>39/8
Vậy tập n là {x/x>39/8}

a) Ta có đồ thị:
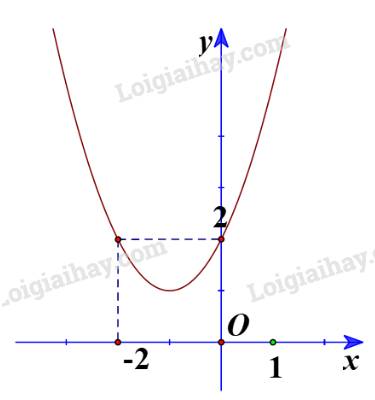
Từ đồ thị ta thấy \({x^2} + 2x + 2 > 0\) biểu diễn phần parabol \(y = {x^2} + 2x + 2\) nằm phía trên trục hoành, tương ứng với mọi \(x \in \mathbb{R}\).
Vậy tập nghiệm của bất phương trình \({x^2} + 2x + 2 > 0\) là \(\mathbb{R}\).
b) Ta có đồ thị:
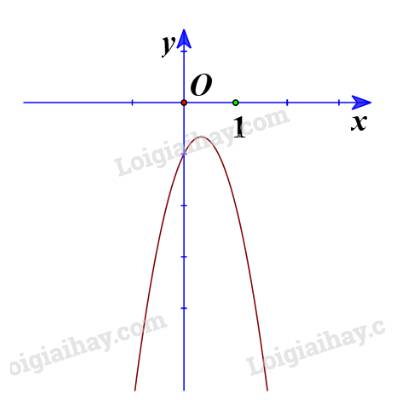
Từ đồ thị ta thấy \( - 3{x^2} + 2x - 1 > 0\) biểu diễn phần parabol \(y = - 3{x^2} + 2x - 1\) nằm phía trên trục hoành, tương ứng với \(x \in \emptyset \)
Vậy tập nghiệm của bất phương trình \( - 3{x^2} + 2x - 1 > 0\) là \(\emptyset \).

\(\dfrac{x}{2x-6}-\dfrac{x}{2x+2}=\dfrac{2x}{\left(x+1\right)\left(x-3\right)}\left(ĐKXĐ:x\ne-1,x\ne3\right)\)
\(\Leftrightarrow\dfrac{x}{2\left(x-3\right)}-\dfrac{x}{2\left(x+1\right)}=\dfrac{2x}{\left(x+1\right)\left(x-3\right)}\)
\(\Leftrightarrow\dfrac{x\left(x+1\right)}{2\left(x+1\right)\left(x-3\right)}-\dfrac{x\left(x-3\right)}{2\left(x+1\right)\left(x-3\right)}=\dfrac{2x\cdot2}{2\left(x+1\right)\left(x-3\right)}\)
\(\Rightarrow x\left(x+1\right)-x\left(x-3\right)=4x\)
\(\Leftrightarrow x^2+x-x^2+3x=4x\)
\(\Leftrightarrow x^2+x-x^2+3x-4x=0\)
\(\Leftrightarrow0x=0\)
Phương trình có vô số nghiệm , trừ x = -1,x = 3
Vậy ...
\(\dfrac{12x+1}{12}< \dfrac{9x+1}{3}-\dfrac{8x+1}{4}\)
\(\Leftrightarrow12\cdot\dfrac{12x+1}{12}< 12\cdot\dfrac{9x+1}{3}-12\cdot\dfrac{8x+1}{4}\)
\(\Leftrightarrow12x+1< 4\left(9x+1\right)-3\left(8x+1\right)\)
\(\Leftrightarrow12x+1< 36x+4-24x-3\)
\(\Leftrightarrow12x+1< 12x+1\)
\(\Leftrightarrow12x-12x< 1-1\)
\(\Leftrightarrow0x< 0\)
Vậy S = {x | x \(\in R\)}

\(\left\{{}\begin{matrix}2X+Y\ge1\left(1\right)\\X-3Y\le1\left(2\right)\end{matrix}\right.\)
*Giải 2X+Y-1=0
cho đi qua 2 điểm và thử điểm O(0;0) vào (1) và loại đi phần k thỏa mãn
*Tương tự giải X-3Y-1=0
*Lấy giao (1) và (2)

\(f\left(x\right)=\dfrac{\left(3x-4\right)\left(2x-3\right)}{\left(x^2-5x+6\right)\left(5-x\right)}>0\)
\(\Leftrightarrow\dfrac{\left(3x-4\right)\left(2x-3\right)}{\left(x-2\right)\left(x-3\right)\left(5-x\right)}>0\)
Bảng xét dấu:
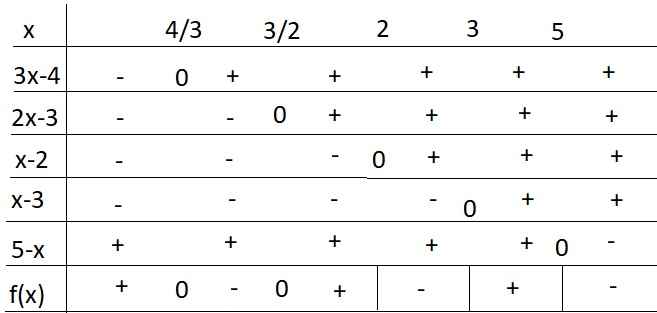
Từ bảng xét dấu ta thấy nghiệm của BPT là: \(\left[{}\begin{matrix}x< 5\\\dfrac{3}{2}< x< 2\\3< x< 5\end{matrix}\right.\)

1:
a: =>3x=6
=>x=2
b: =>4x=16
=>x=4
c: =>4x-6=9-x
=>5x=15
=>x=3
d: =>7x-12=x+6
=>6x=18
=>x=3
2:
a: =>2x<=-8
=>x<=-4
b: =>x+5<0
=>x<-5
c: =>2x>8
=>x>4

4: =>2x-3>5 hoặc 2x-3<-5
=>x>4 hoặc x<-1
5: =>-4<=2x-1<=4
=>-3/2<=x<=5/2

b, ĐK: \(x\ne8\)
\(A=\dfrac{x-5}{x-8}>0\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x-5>0\\x-8>0\end{matrix}\right.\\\left\{{}\begin{matrix}x-5< 0\\x-8< 0\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x>5\\x>8\end{matrix}\right.\\\left\{{}\begin{matrix}x< 5\\x< 8\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x>8\\x< 5\end{matrix}\right.\)
\(\Rightarrow\orbr{\begin{cases}2x-4=6\\2x-4=-6\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}x=5\\x=-1\end{cases}}\)
Vậy ...
em chỉ làm đc thôi chứ cách gì em ko bít đâu