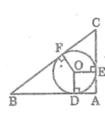
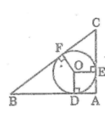
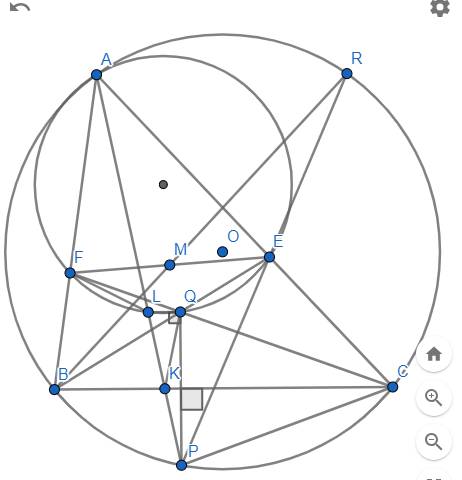
cho tam giác ABC nội tiếp (O) đk AB sao cho AC<BC; E là 1 điểm thuộc BC (E khác B,C). Tia AE cắt (O) tại D. EH vuông AB tại H
1. CM ACEH là tứ giác nội tiếp
2, CH cắt (O) tại F, CM EH//DF
3.CM đg tròn ngoại tiếp tam giác CHO đi qua D
4. Gọi I, K lần lượt là hình chiếu vuông góc của F trên đg thẳng CA và CB. CM AB,DF,IK cùng đi qua 1 điểm