Viết tất cả các phân số tối giản a/b(a>0,b>0)biết a.b=36
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
2L
3
26 tháng 2 2021
Ta thấy : \(\text{Ư}\left(36\right)=\left\{\pm1;\pm2;\pm3;\pm4;\pm6;\pm12;\pm18;\pm36\right\}\)
Vì \(\frac{a}{b}\)tối giản và a.b = 36 nên được: \(\frac{1}{36};\frac{-1}{-36}\)
Vậy \(\frac{a}{b}=\left\{\frac{1}{36};\frac{-1}{-36}\right\}\)
#Chúc em học tốt
HP
1
22 tháng 8 2019
Ta thấy: \(Ư\left(36\right)=\left\{1\pm;\pm2;\pm3;\pm4;\pm6;\pm9;\pm12;\pm18;\pm36\right\}\)
Vì tối giản nên viết đc: \(\frac{1}{36};\frac{-1}{-36}\)
Các p/s khác viết đc nhưng k tối giản hoặc tối giản nhưng ab k = 36
Hội con 🐄 chúc bạn học tốt!!!
AB
2
L
28 tháng 1 2022
ta có U( 36) = { 1;-1;2;-2;3;-3;4;-4;6;-6;9;-9;12;-12;36;-36}
mà a phần b tối giản ; ab = 36
=> a/b = 1/ 36 = -1/36
CM
3 tháng 7 2019
Đặt x + 1 t = t , t ≥ 2 khi đó phương trình trở thành 2 t 2 − 3 t − 5 m − 3 = 0 ( * )
Phương trình 2 x 2 + 1 x 2 - 3 x + 1 x - 5 m + 1 = 0 có nghiệm khi và chỉ khi phương trình (*) có nghiệm t thỏa mãn t ≥ 2
Số nghiệm của phương trình (*) bằng số giao điểm của parabol (P): y = 2 t 2 − 3 t − 3 và đường thẳng d : y = 5 m
Xét parabol P : y = 2 t 2 - 3 t - 3 ta có bảng biến thiên như sau:
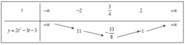
Từ bảng biến thiên ta có phương trình (*) có nghiệm t ∈ ( - ∞ ; - 2 ] ∪ [ 2 ; + ∞ ) khi và chỉ khi 5 m ≥ - 1 hoặc 5 m ≥ 11
Vậy khi m ∈ − 1 5 ; + ∞ thì phương trình có nghiệm ⇒ a = 1 b = 5 ⇒ T = 5
Đáp án cần chọn là: B
CM
26 tháng 8 2019
Điều kiện xác định: x ≠ 0 .
Đặt t = x + 1 x ⇒ t 2 − 2 = x 2 + 1 x 2 ≥ 2 ⇒ t ≥ 2 ⇔ t ≥ 2 t ≤ − 2
Phương trình đã cho trở thành 2 t 2 − 2 − 3 t − 2 m + 1 = 0
⇔ 2 t 2 − 3 t − 2 m − 3 = 0 ⇔ 2 t 2 − 3 t − 3 = 2 m ( 1 )
Xét hàm số y = f ( t ) = 2 t 2 − 3 t − 3 có bảng biến thiên:
(1) Có nghiệm t thỏa mãn
t
≥
2
t
≤
−
2
k
h
i
2
m
≥
−
1
2
m
≥
11
⇔
m
≥
−
1
2
⇒
S
=
−
1
2
;
+
∞
Vậy T = 3
Đáp án cần chọn là: D
LG
0
L
1