Cho \(\Delta ABC\) , AB=5, AC=6, \(\widehat{A}=90^o+\frac{\widehat{B}}{2}\) . tính BC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HT
0
3 tháng 12 2018
A C B E D Xét tam giác vuông ABC và tam giác vuông ADE có :
AB=AD
AC=AE
=> tam giác ABC= tam giác ADE ( 2 cạnh góc vuông )
23 tháng 9 2020
Vẽ phân giác BD, ta có: \(\frac{DA}{DC}=\frac{BA}{BC}\)
\(\Rightarrow\frac{DA}{AB}=\frac{DC}{BC}=\frac{DA+DC}{AB+BC}=\frac{AC}{AB+BC}\left(1\right)\)
Mặt khác \(\Delta ABD\)vuông tại A, ta có:
\(\tan\widehat{ABD}=\tan\frac{\widehat{ABC}}{2}=\frac{DA}{AB}\left(2\right)\)
Từ (1) và (2) =>đpcm
TM
3
NV
Nguyễn Việt Lâm
Giáo viên
28 tháng 3 2023
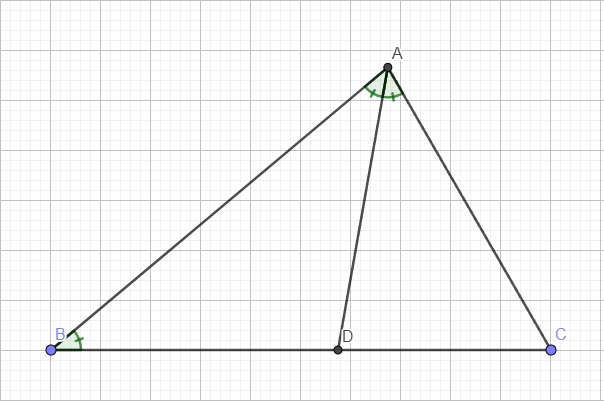
Kẻ phân giác AD (D thuộc BC)
\(\Rightarrow\widehat{B}=\widehat{BAD}=\widehat{CAD}=\dfrac{\widehat{A}}{2}\)
Xét hai tam giác ABC và DAC có:
\(\left\{{}\begin{matrix}\widehat{C}\text{ chung}\\\widehat{B}=\widehat{CAD}\end{matrix}\right.\) \(\Rightarrow\Delta ABC\sim\Delta DAC\left(g.g\right)\)
\(\Rightarrow\dfrac{AC}{DC}=\dfrac{BC}{AC}\Rightarrow DC=\dfrac{AC^2}{BC}=\dfrac{27}{4}\)
\(\Rightarrow BD=BC-DC=\dfrac{21}{4}\)
Áp dụng định lý phân giác:
\(\dfrac{BD}{AB}=\dfrac{DC}{AC}\Rightarrow AB=\dfrac{BD.AC}{DC}=7\)
