cho đường thẳng d2 : 3X +5Y-9
Đường thẳng (d1) đi qua điểm N(-3;1) và vuông góc với d2. Tìm phương trình tổng quát của đt d1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

*Đường thẳng ( d 1 ): ax + 2y = -3 đi qua điểm M(3; 9) nên tọa độ điểm M nghiệm đúng phương trình đường thẳng.
Ta có: a.3 + 2.9 = -3 ⇔ 3a + 18 = -3 ⇔ 3a = -21 ⇔ a = -7
Phương trình đường thẳng ( d 1 ): -7x + 2y = -3
*Đường thẳng ( d 2 ): 3x – by = 5 đi qua điểm N(-1; 2) nên tọa độ điểm N nghiệm đúng phương trình đường thẳng.
Ta có: 3.(-1) – b.2 = 5 ⇔ -3 – 2b = 5 ⇔ 2b = -8 ⇔ b = -4
Phương trình đường thẳng ( d 2 ): 3x + 4y = 5
*Tọa độ giao điểm của (
d
1
) và (
d
2
) là nghiệm của hệ phương trình: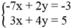
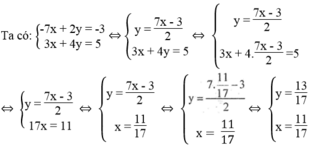

Tọa độ giao điểm của hai đường thẳng (
d
1
): 2x + 5y = 17, (
d
2
): 4x – 10y = 14 là nghiệm của hệ phương trình: 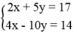
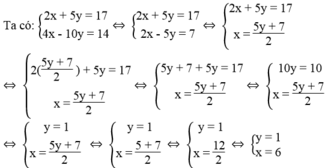
Khi đó ( d 1 ) và ( d 2 ) cắt nhau tại N(6; 1).
Đường thẳng ax – 8y = b đi qua điểm M(9; -6) và N(6;1) nên tọa độ của M và N nghiệm đúng phương trình đường thẳng.
*Điểm M: 9a + 48 = b
*Điểm N: 6a – 8 = b
Khi đó a và b là nghiệm của hệ phương trình: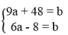
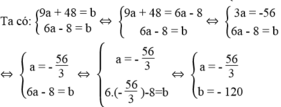
Vậy khi a = - 56/3 , b = -120 thì đường thẳng ax – 8y = b đi qua điểm M(9; -6) và đi qua giao điểm của hai đường thẳng ( d 1 ): 2x + 5y = 17, ( d 2 ): 4x – 10y = 14.

Ta có: (d2): y=3x-2y=1 => y: 3x-2y-1
Phương trình tung độ giao điểm của (d1) và (d2) là:
3x-2 = 3x-2y-1 => 3x-3x+2y=-1+2 => 2y=1 => y = 1/2
=> x = (1/2+2):3 = 5/6
Vậy (d1) và (d2) cùng đi qua điểm C(5/6; 1/2)
Thay x = 5/6 và y = 1/2 vào (d3) ta được: 1/2 = (m-2).5/6+2m-3
=> 1/2 = 5/6m - 5/3 + 2m - 3
=> 31/6 = 17/6 m
=> m = 31/17
Vậy m = 31/17 thì 3 đường thẳng (d1);(d2);(d3) cùng đi qua 1 điểm

+ (d): ax-8y=b ⇒ (d): 8y = ax-b
Ta có: (d): 8y=ax-b đi qua M(9; -6)
⇒ thay \(\left\{{}\begin{matrix}x=9\\y=-6\end{matrix}\right.\) vào 8y = ax-b, ta được:
8 *(-6) = 9a-b ⇔ - 48 = 9a-b (*)
+ (d1): 2x+5y=17 ⇒ (d1): 5y= -2x+17
(d2) : 2x-5y=7 ⇒ 5y=2x-7
Ta có phương trình hoành độ giao điểm của (d1) và (d2):
-2x+17 = 2x-7 ⇔ 4x=24 ⇔ x=6
⇒ y= 1
Gọi N là giao điểm của (d1) và (d2), ta có: N(6;1)
⇒ thay \(\left\{{}\begin{matrix}x=6\\y=1\end{matrix}\right.\) vào 8y = ax -b, ta được: 8= 6a-b (**)
Từ (*) và (**), ta có hpt:
\(\left\{{}\begin{matrix}-48=9a-b\\8=6a-b\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3a=-56\\b=6a-8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-\dfrac{56}{3}\\b=-120\end{matrix}\right.\)
Vậy \(\left\{{}\begin{matrix}a=-\dfrac{56}{3}\\b=-120\end{matrix}\right.\)

đt d2 : 3x - 2y = 1 => y = 3/2x - 1/2
Hai đt d1 và d2 có hệ số góc khác nhau nên chúng cắt nhau tại điểm M.Xét pt hoành độ : 3x - 2 = 3/2x - 1/2 <=> x = 1 => y = 1.
Vậy tọa độ điểm \(M\left(1;1\right)\)
Để cho d1,d2,d3 cùng đi qua 1 điểm thì d3 phải di qua M.
\(\Rightarrow\left(d_3\right)\in M\Leftrightarrow1=\left(m-2\right).1+2m-3\Leftrightarrow m=2\)
Vậy ...

a, pt hoanh độ giao điểm cua 2 đg thẳng d1 và d2 la: 2x - 5 = 1 <=> x = 3
vậy tọa độ giao điểm cua d1 va d2 la A(3;1)
Để d1 , d2, d3 đồng quy thì d3 phải đi qua diem A(3;1)
Ta co pt: (2m - 3).3 - 1 = 1
<=> 6m - 9 -1 = 1
<=> 6m = 11 <=> m = 11/6
mấy bài còn lại tương tự nha

(d3): \(3x+2y=1\Rightarrow y=-\frac{3}{2}x+\frac{1}{2}\)
Phương trình tọa độ giao điểm A của (d1) và (d2):
\(\left\{{}\begin{matrix}y=5x-3\\y=-2x+4\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=1\\y=2\end{matrix}\right.\) \(\Rightarrow A\left(1;2\right)\)
Gọi pt (d) có dạng \(y=ax+b\)
Do (d) qua A và song song với (d3) nên:
\(\left\{{}\begin{matrix}a=-\frac{3}{2}\\a+b=2\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=-\frac{3}{2}\\b=\frac{7}{2}\end{matrix}\right.\) \(\Rightarrow y=-\frac{3}{2}x+\frac{7}{2}\)

a) Tìm toạ độ giao điểm A của hai đường thẳng y = 3x - 2 (d1) và y = (2/3)x (d2):
Để tìm toạ độ giao điểm A của hai đường thẳng, ta có thể giải hệ phương trình sau:y = 3x - 2
y = (2/3)x
(2/3)x = 3x - 2
Giải phương trình này, ta được x = 3/4.Thay x = 3/4 vào phương trình y = (2/3)x, ta được y = (2/3)(3/4) = 7/4.Vậy toạ độ giao điểm A của hai đường thẳng (d1) và (d2) là A(3/4, 7/4).b) Viết phương trình đường thẳng (d) đi qua A và song song với đường thẳng (d3) là y = 3x - 1:
Để viết phương trình đường thẳng (d) đi qua A và song song với đường thẳng (d3), ta có thể sử dụng công thức sau:y - y0 = m(x - x0)
Trong đó, (x0, y0) là toạ độ của điểm A và m là hệ số góc của đường thẳng (d3).
Thay các giá trị này vào công thức trên, ta được:y - 7/4 = 3(x - 3/4)
Sau khi sắp xếp lại các số hạng, ta được phương trình đường thẳng (d) là: y = 3x - 5/4.