tìm các số tự nhiên x,y t/m
2x+1=y2
Giups mk đi mà
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
18 tháng 6 2016
A) Tập hợp A có 1 phần tử đó là 16
B) Tập hợp B có 1 phần tử đó là 0
C) Tập hợp C có vô số phần tử
D) Tập hợp D không có phần tử nào hay còn gọi là tập hợp rỗng
2 tháng 11 2016
a)B(11)={11;22;33;44}
b)Ư(33)={1;3}
c)B(11) Ư(33)={11;33}
19 tháng 6 2018
A = {14}
=> A có 1 phần tử
B = {-1}
=> B có 1 phần tử
C = {13}
=> C có 1 phần tử
D = {1; 2; 3; 4;...}
=> D có vô số phần tử
19 tháng 6 2018
trả lời:
a) A=[14]
=> A có 1 phần tử
b) B= [-1]
=> B có 1 phần tử
c)C= [1;2;3;4;...]
=> D có vô số phần tử
học tốt!!!!!!!!!!!
CM
19 tháng 2 2017
Chọn D
Xét 
.
Tập xác định 
.
Ta có: 
.
Hàm số đạt cực tiểu tại 
nên 
.
Ta có 
.
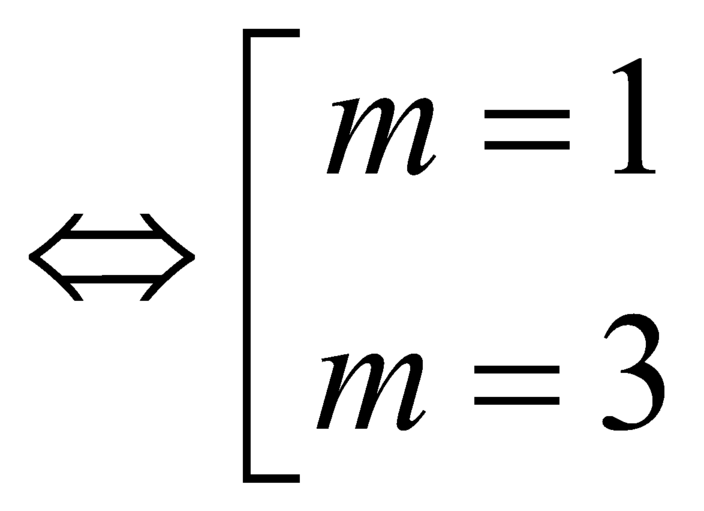Thử lại:
* Với 
, ta có:
.
.
.
và 
.
Do đó hàm số hàm số đạt cực tiểu tại 
.
* Với 
, ta có:
.
.
.
và 
.
Do đó hàm số hàm số không đạt cực tiểu tại x=1
Vậy với m= 1, hàm số đạt cực tiểu tại x = 1
7 tháng 9 2021
a: A={4}
A có 1 phần tử
b: B={0;1}
B có 2 phần tử
c: \(C=\varnothing\)
C không có phần tử nào
d: D={0}
D có 1 phần tử
e: E={x|\(x\in N\)}
E có vô số phần tử
TA CÓ:
\(2^x+1=y^2\)
=> \(2^x=y^2-1^2\)(do 1 lũy thừa lên bao nhiêu cũng bằng 1)
=> \(2^x=\left(y-1\right)\left(y+1\right)\)
=> 2 = (y+1) - (y-1)
=> y - 1 = 2
=> y = 3 => x = 3
chúc bn học tốt !
chỗ nào ko hiểu thì hỏi nha