so sánh
A= 1718 + 1 phần 1719 + 1
và B = 1717 + 1 phần 1718 +1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tính A=17/18+1718/1718+171717/181818+...+1717...17/1818...18(2018 chữ số 17 và 18). Ai làm đc tk cho

\(A=\frac{17}{18}+\frac{1717}{1818}+\frac{171717}{181818}+...+\frac{1717..17}{1818...18}\)(2018 số 17 và 18)
\(=\frac{17}{18}+\frac{17.101}{18.101}+\frac{17.10101}{18.10101}+...+\frac{17.1010...01}{18.1010...01}\)(2017 cặp số 10 liên tiếp và dư 1 số 1)
\(=\frac{17}{18}+\frac{17}{18}+\frac{17}{18}+...+\frac{17}{18}\left(2018\text{ số hạng}\right)\)
\(=\frac{17}{18}.2018=\frac{17153}{9}\)

Hướng dẫn giải:
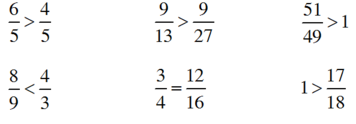
Giải thích:
+ 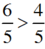 vì cùng có mẫu bằng 5, tử số 6 > 4.
vì cùng có mẫu bằng 5, tử số 6 > 4.
+ 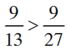 vì có cùng tử số, mẫu số 13 < 27.
vì có cùng tử số, mẫu số 13 < 27.
+ 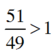 vì tử số 51 > mẫu số = 49.
vì tử số 51 > mẫu số = 49.
+ 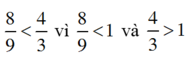
+ 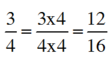
+ 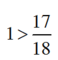 vì tử số bằng 17 < mẫu số bằng 18.
vì tử số bằng 17 < mẫu số bằng 18.

1/3+1/15+1/35+1/63+1/99+1/143+1/195
=1/1*3+1/3*5+1/5*7+1/7*9+1/9*11+1/11*13+1/13*15
suy ra 2(1/1*3+1/3*5+1/5*7+1/7*9+1/9*11+1/11*13+1/13*15)
=2/1*3+2/3*5+2/5*7+2/7*9+2/9*11+2/11*13+2/13*15
=1-1/3+1/3-1/5+1/5-1/7+1/7-1/9+1/9-1/11+1/11-1/13+1/13-1/15
=1-1/15
=14/15
a=14/15 chia 2=7/15

Ta có: 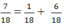
Ta có thể ghép hai miếng bìa 1/18 và 6/18 lại với nhau để được 7/18 hình tròn.
Ta có: 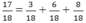
Ta có thể ghép ba miếng bìa 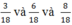 lại với nhau để được 17/18 hình tròn.
lại với nhau để được 17/18 hình tròn.
Ta có: 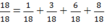
Ghép tất cả các miếng lại với nhau để được 18/18 hình tròn

Ta có : \(\dfrac{1}{2}< \dfrac{1}{1.2};\dfrac{1}{2^2}< \dfrac{1}{2.3};...;\dfrac{1}{2^{10}}< \dfrac{1}{9.10}\)
\(\Rightarrow\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{10}}< \dfrac{1}{1.2}+\dfrac{1}{2.3}+...+\dfrac{1}{9.10}\)
\(=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{9}-\dfrac{1}{10}=\dfrac{9}{10}< 1\Rightarrow A< B\)

3.
A:
20032003+1=20032002.2003+1=20032002+1
20032004+1=20032002.2003.2003+1=20032002.2003+1(loại số 2003 thứ hai của cả mẫu số và tử số)
B:
20032002+1=20032002+1
20032003+1=20032002.2003+1
Suy ra: A=B
Ta có A=17^18+1/17^19+1 < 17^18+1+16/17^19+1+16 = 17^18+17/17^19+17 = 17(17^17+1/17^18+1)= B
Vậy A<B
\(A=\frac{17^{18}+1}{17^{19}+1}\)
Ta có : \(17A=\frac{17(17^{18}+1)}{17^{19}+1}=\frac{17^{19}+17}{17^{19}+1}=\frac{17^{19}+1+16}{17^{19}+1}=1+\frac{17}{17^{19}+1}\) \((1)\)
\(B=\frac{17^{17}+1}{17^{18}+1}\)
Ta lại có : \(17B=\frac{17(17^{17}+1)}{17^{18}+1}=\frac{17^{18}+17}{17^{18}+1}=\frac{17^{18}+1+16}{17^{18}+1}=1+\frac{17}{17^{18}+1}\) \((2)\)
Từ 1 và 2 suy ra : \(1+\frac{16}{17^{19}+1}< 1+\frac{16}{17^{18}+1}\)
Nên \(17A< 17B\)
Hay \(A< B\)
Vậy : \(A< B\)