Với a>0, b>0, b#1/4, rút gọn bt: \(\frac{a+\sqrt{a}+\frac{1}{4}}{2\sqrt{a}+1}\) : \(\frac{4b-1}{8\sqrt{b}-4}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
14 tháng 8 2023
a: \(\sqrt{5a^2}=\left|a\sqrt{5}\right|=-a\sqrt{5}\left(a< =0\right)\)
c: A=\(\sqrt{72a^2b^4}=\sqrt{36a^2b^4\cdot2}=6\sqrt{2}\cdot b^2\cdot\left|a\right|\)
mà a<0
nên \(A=-6\sqrt{2}\cdot ab^2\)
d: \(\sqrt{24a^4b^8}=\sqrt{4a^4b^8\cdot6}=2a^2b^4\cdot\sqrt{6}\)
9 tháng 6 2016
b, \(a+b+2\sqrt{a.b}=\sqrt{a^2}+\sqrt{b^2}+2\sqrt{ab}=\left(\sqrt{a}+\sqrt{b}\right)^2\) ( Vì a, b >= 0 )
c, \(a+b-2\sqrt{a.b}=\sqrt{a^2}+\sqrt{b^2}-2\sqrt{ab}=\left(\sqrt{a}-\sqrt{b}\right)^2\)( Vì a, b >= 0 )
CM
18 tháng 8 2018
Đáp án B
Do đường tròn (C) tiếp xúc với đường thẳng AB tại B và tiếp xúc với đường thẳng AC tại C
Nên tam giác ABC cân tại A
tâm I của (C) thuộc Oy nên I(0; y0)
Do:
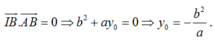
Mặc khác:
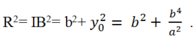
Vậy phương trình của là:
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 5 2019
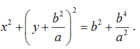
\(AB=AC=\sqrt{a^2+b^2}\) (1)
Do (C) tiếp xúc AB tại B và AC tại C \(\Rightarrow IA=IB=R\) (2)
Từ (1) và (2) \(\Rightarrow IA\) là trung trực của BC
Mà B và C nằm trên Ox, A nằm trên Oy \(\Rightarrow I\) nằm trên Oy \(\Rightarrow I\left(0;y\right)\)
\(\Rightarrow IA=y_A-y_I=a-y\)
Theo hệ thức lượng ta có:
\(IA.OA=AB^2\Leftrightarrow IA=\frac{AB^2}{OA}\Leftrightarrow a-y=\frac{a^2+b^2}{a}\)
\(\Rightarrow y=a-\frac{a^2+b^2}{a}=\frac{-b^2}{a}\Rightarrow I\left(0;-\frac{b^2}{a}\right)\)
H
0
17 tháng 6 2021
`(asqrtb-bsqrta)/sqrt{ab}-(a-b)/(sqrta-sqrtb)`
`=(sqrt{ab}(\sqrta-sqrtb))/sqrt{ab}-((sqrta-sqrtb)(sqrta+sqrtb))/(sqrta-sqrtb)`
`=sqrta-sqrtb-(sqrta-sqrtb)`
`=-2sqrtb`
TA
17 tháng 6 2021
`(a\sqrtb-b\sqrta)/(\sqrt(ab)) -(a-b)/(\sqrta-\sqrtb)`
`=(\sqrt(ab) (\sqrta-\sqrtb))/(\sqrt(ab)) - ((\sqrta-\sqrtb)(\sqrta+\sqrtb))/(\sqrta-\sqrtb)`
`=(\sqrta-\sqrtb) - (\sqrta+\sqrtb)`
`=-2\sqrtb`
TT
14 tháng 8 2020
a)
Với A=0
\(\Rightarrow x\left(x-4\right)=0\)
\(\Rightarrow\orbr{\begin{cases}x=0\\x-4=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=0\\x=4\end{cases}}}\)
với A<0
\(\Rightarrow x\left(x-4\right)< 0\)
\(th1\orbr{\begin{cases}x< 0\\x-4>0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x< 0\\x>4\end{cases}\Leftrightarrow4< x< 0\left(vl\right)}\)
\(th2\orbr{\begin{cases}x>0\\x-4< 0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x>0\\x< 4\end{cases}\Leftrightarrow0< x< 4\left(tm\right)}\)
\(\Leftrightarrow0< x< 4\Leftrightarrow x\in\left\{1;2;3\right\}\)
Với A>0
\(\Rightarrow x\left(x-4\right)>0\)
\(th1\orbr{\begin{cases}x>0\\x-4>0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x>0\\x>4\end{cases}}\Leftrightarrow x>4\)
\(th2\orbr{\begin{cases}x< 0\\x-4< 0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x< 0\\x< 4\end{cases}}\Leftrightarrow x< 0\)
TT
14 tháng 8 2020
b)
Với B=0
\(\Rightarrow\frac{x-3}{x}=0\)
\(\Leftrightarrow\orbr{\begin{cases}x-3=0\Rightarrow x=3\\x=0\left(l\right)\end{cases}}\)
vậy x=3 thì B = 0
Với B < 0
\(\Rightarrow\frac{x-3}{x}< 0\)
\(th1\orbr{\begin{cases}x-3>0\\x< 0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x>3\\x< 0\end{cases}\Leftrightarrow3< x< 0\left(vl\right)}\)
\(th2\orbr{\begin{cases}x-3< 0\\x>0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x< 3\\x>0\end{cases}\Leftrightarrow0< x< 3\left(tm\right)\Leftrightarrow x\in\left\{1;2\right\}}\)
Với B > 0
\(th1\orbr{\begin{cases}x-3>0\\x>0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x>3\\x>0\end{cases}\Leftrightarrow x>3}\)
\(th2\orbr{\begin{cases}x-3< 0\\x< 0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x< 3\\x< 0\end{cases}\Leftrightarrow x< 0}\)
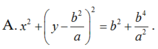
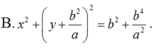
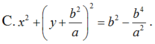
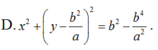
\(P=\frac{\frac{1}{4}\left(4a+4\sqrt{a}+1\right)}{2\sqrt{a}+1}.\frac{4\left(2\sqrt{b}-1\right)}{\left(2\sqrt{b}\right)^2-1}\)
\(P=\frac{\left(2\sqrt{a}+1\right)^2}{\left(2\sqrt{a}+1\right)}.\frac{\left(2\sqrt{b}-1\right)}{\left(2\sqrt{b}-1\right)\left(2\sqrt{b}+1\right)}\)
\(P=\frac{2\sqrt{a}+1}{2\sqrt{b}-1}\)