Cho phương trình bậc hai (ẩn x): x^2-4x+m+2=0 (1). a) giải phương trình (1) khi m=1 . b) Giả sử phương trình (1) có nghiệm hãy tính giá trị của m để x1-x2=6 .
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
23 tháng 2 2022
a, Thay m=3 vào pt ta có:
\(\left(1\right)\Leftrightarrow x^2-6x+4=0\\ \Leftrightarrow x=3\pm\sqrt{5}\)
b, Để pt có 2 nghiệm thì \(\Delta'\ge0\)
\(\Leftrightarrow\left(-m\right)^2-1.4\ge0\\ \Leftrightarrow m^2-4\ge0\\ \Leftrightarrow\left[{}\begin{matrix}m\ge2\\m\le-2\end{matrix}\right.\)
Theo Vi-ét:\(\left\{{}\begin{matrix}x_1+x_2=2m\\x_1x_2=4\end{matrix}\right.\)
\(\left(x_1+1\right)^2+\left(x_2+1\right)^2=2\\ \Leftrightarrow x^2_1+2x_1+1+x^2_2+2x_2+1=2\\ \Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2+2\left(x_1+x_2\right)=0\\ \Leftrightarrow\left(2m\right)^2-2.4+2.2m=0\\ \Leftrightarrow4m^2+4m-8=0\\ \Leftrightarrow\left[{}\begin{matrix}m=1\left(ktm\right)\\m=-2\left(tm\right)\end{matrix}\right.\)
23 tháng 3 2022
a)thay m=1 vào pt ta có
\(x^2+4x=0\)
<=> \(\left[{}\begin{matrix}x=0\\x=-4\end{matrix}\right.\)
b) thay x=2 vào pt ta có: 13+m=0
<=>m=-13
thay m=-13 vào pt ta có
\(x^2+4x-12=0\)
<=>(x-2)(x+6)=0
<=>\(\left[{}\begin{matrix}x=2\\x=-6\end{matrix}\right.\)\(\)
vậy với m=-13 thì nghiệm còn lại là x=-6
c) để pt có 2 nghiệm pb thì \(\Delta>0\)
<=>16-4m-4>0
<=>3-m>0
<=>m<3
áp dụng định lí Vi-ét ta có\(\left\{{}\begin{matrix}x_1+x_2=-4\\x_1x_2=m+1\end{matrix}\right.\)
theo đề bài ta có \(x_1^2+x_2^2=10\)
<=>\(\left(x_1+x_2\right)^2-2x_1x_2=10\)
<=>16-2m-2=10
<=>2-m=0
<=>m=2(nhận)
vậy với m=2 thì pt có 2 nghiệm pb thỏa yêu cầu đề bài.
23 tháng 2 2022
a, Thay m=0 vào pt ta có:
\(x^2-x+1=0\)
\(\Rightarrow\) pt vô nghiệm
b, Để pt có 2 nghiệm thì \(\Delta\ge0\)
\(\Leftrightarrow\left(-1\right)^2-4.1\left(m+1\right)\ge0\\ \Leftrightarrow1-4m-4\ge0\\ \Leftrightarrow-3-4m\ge0\\ \Leftrightarrow4m+3\le0\\ \Leftrightarrow m\le-\dfrac{3}{4}\)
Theo Vi-ét:\(\left\{{}\begin{matrix}x_1+x_2=1\\x_1x_2=m+1\end{matrix}\right.\)
\(x_1x_2\left(x_1x_2-2\right)=3\left(x_1+x_2\right)\\ \Leftrightarrow\left(x_1x_2\right)^2-2x_1x_2=3.1\\ \Leftrightarrow\left(m+1\right)^2-2\left(m+1\right)-3=0\\ \Leftrightarrow\left[{}\begin{matrix}m+1=3\\m+1=-1\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}m=2\left(ktm\right)\\m=-2\left(tm\right)\end{matrix}\right.\)
H
3 tháng 5 2023
a, Thay \(m=1\) vào \(\left(1\right)\)
\(\Rightarrow x^2-7x+1=0\\ \Delta=\left(-7\right)^2-4.1.1=45\\ \Rightarrow\left\{{}\begin{matrix}x_1=\dfrac{7+3\sqrt{5}}{2}\\x_2=\dfrac{7-3\sqrt{5}}{2}\end{matrix}\right.\)
b, \(\Delta=\left(-7\right)^2-4.m=49-4m\)
phương trình cs nghiệm \(49-4m\ge0\\ \Rightarrow m\le\dfrac{49}{4}\)
Áp dụng hệ thức vi ét
\(\left\{{}\begin{matrix}x_1+x_2=7\\x_1x_2=m\end{matrix}\right.\)
\(x^2_1+x^2_2=29\\ \Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=29\\ \Leftrightarrow7^2-2.m-29=0\\ \Leftrightarrow20-2m=0\\ \Rightarrow m=10\left(t/m\right)\)
Vậy \(m=10\)
CM
23 tháng 10 2019
a. + Với m = − 1 2 phương trình (1) trở thành x 2 − 4 x = 0 ⇔ x = 0 x = 4 .
+ Vậy khi m = − 1 2 phương trình có hai nghiệm x= 0 và x= 4.
b. + Phương trình có hai nghiệm dương phân biệt khi
Δ = 2 m + 5 2 − 4 2 m + 1 > 0 x 1 + x 2 = 2 m + 5 > 0 x 1 . x 2 = 2 m + 1 > 0
+ Ta có Δ = 2 m + 5 2 − 4 2 m + 1 = 4 m 2 + 12 m + 21 = 2 m + 3 2 + 12 > 0 , ∀ m ∈ R
+ Giải được điều kiện m > − 1 2 (*).
+ Do P>0 nên P đạt nhỏ nhất khi P 2 nhỏ nhất.
+ Ta có P 2 = x 1 + x 2 − 2 x 1 x 2 = 2 m + 5 − 2 2 m + 1 = 2 m + 1 − 1 2 + 3 ≥ 3 ( ∀ m > − 1 2 ) ⇒ P ≥ 3 ( ∀ m > − 1 2 ) .
và P = 3 khi m= 0 (thoả mãn (*)).
+ Vậy giá trị nhỏ nhất P = 3 khi m= 0.
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 3 2022
a. Với \(m=-5\) pt trở thành:
\(x^2+8x-9=0\)
\(a+b+c=1+8-9=0\) nên pt có 2 nghiệm: \(\left\{{}\begin{matrix}x_1=1\\x_2=-9\end{matrix}\right.\)
b. Ta có:
\(\Delta'=\left(m+1\right)^2-\left(m-4\right)=m^2+m+5=\left(m+\dfrac{1}{2}\right)^2+\dfrac{19}{4}>0;\forall m\)
\(\Rightarrow\) Pt đã cho luôn có 2 nghiệm pb với mọi m
18 tháng 6 2023
a: Khi m=5 thì (1) sẽ là: x^2+5x+4=0
=>x=-1; x=-4
b: Sửa đề: Q=x1^2+x2^2-4x1-4x2
Q=(x1+x2)^2-2x1x2-4(x1+x2)
=m^2-2(m-1)-4(-m)
=m^2-2m+2+4m
=m^2+2m+2=(m+1)^2+1>=1
Dấu = xảy ra khi m=-1
CM
10 tháng 8 2018
a) Với m = 1 phương trình trở thành:
x 2 + 4x + 4 = 0 ⇔ (x + 2 ) 2 = 0 ⇔ x = -2
Vậy x = -2
b) Ta có: Δ' = m 2 - 5m + 4
Phương trình có hai nghiệm phân biệt
⇔ Δ' > 0 ⇔
m
2
- 5m + 4 > 0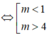 
Do x1 < x2 < 1
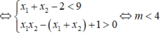
a/ Bạn tự giải
b/ \(\Delta'=4-m-2=2-m\ge0\Rightarrow m\le2\)
Khi đó, phương trình có 2 nghiệm thỏa mãn: \(\left\{{}\begin{matrix}x_1+x_2=4\\x_1x_2=m+2\end{matrix}\right.\)
Kết hợp điều kiện đề bài ta có hệ:
\(\left\{{}\begin{matrix}x_1-x_2=6\\x_1+x_2=4\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_1=5\\x_2=-1\end{matrix}\right.\)
Mà \(x_1x_2=m+2\Rightarrow m+2=5.\left(-1\right)=-5\Rightarrow m=-7\)