người ta dùng 1 bếp điện để đun nước chứa trong ấm. Biết nhiệt lượng do bếp cung cấp cho nước là không đổi. Nhiệt độ ban đầu của nước là 20oc. Thời gian từ lúc bắt đầu đun nước cho đến khi sôi là 15 phút. Khi nước bắt đâù sôi thì ngừng đun, sau khi ngừng đun nước 30 phút thì Nhiệt độ nước trong ấm là 60oC. Cho rằng khi đun và để nguôi nước nhiệt lượng tỏa ra môi trường trong 1 đơn vị thời gian là đều đặn. Tìm hiệu suất nhiệt của bếp khi đun? Cho NDR của nước là 42000 J/kg.K
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Nhiệt lượng cần cung cấp để đun sôi lượng nước trên là:
Q1 = c.m.(T – T0) = 4200.2.(100 - 20) = 672000 (J)
b) Hiệu suất của bếp: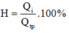
Nhiệt lượng mà ấm điện đã tỏa ra khi đó là:
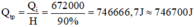
c) Từ công thức: Qtp = A = P.t
→ Thời gian đun sôi lượng nước:
a) Nhiệt lượng cần cung cấp để đun sôi lượng nước trên là:
Q1 = c.m.(T – T0) = 4200.2.(100 - 20) = 672000 (J)
b) Hiệu suất của bếp: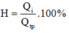

Đổi 1 , 5 l = 1 , 5 . 10 - 3 m 3 ⇒ m = D.V = 1000. 1,5. 10 - 3 = 1,5 kg
Đổi 20 phút = 1200 giây
a) Công suất tỏa nhiệt của bếp là: P = I 2 . R = 2,52. 80 = 500 (W)
b) Nhiệt lượng thu vào của nước từ 25 o C đến 100 o C là:
Q 1 = m . c . ( t 2 - t 1 ) = 1,5. 4200. (100 - 25) = 472500 (J)
Nhiệt lượng mà bếp tỏa ra trong 20 phút là:
Q t p = I 2 . R . t = 2,52. 80. 1200 = 600000(J)
Hiệu suất của bếp là:
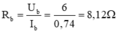

a). Nhiệt lượng cần cung cấp để đun sôi nước:
\(Q_{thu}=m.c\left(t_2-t_1\right)\)
⇒\(1,5.4200.\left(100-25\right)\)
⇒ \(472500\left(J\right)\)
12 phút = 720s
\(Q_{toả}=I^2.R.t\)
⇒\(5^2.44.720\)
⇒ \(792000\)(J)
Hiệu suất của bếp là:
\(H=\dfrac{Q_i}{Q_{tp}}\).100%= \(\dfrac{472500}{792000}.100\%=59,66\%\)
b). 3 giờ=10800s
Hiệu điện thế qua bếp điện là:
\(U=I.R=5.44=220V\)
Công của dòng điện:
\(A=U.I.t=220.5.10800.30=356400000\left(J\right)\)
\(=99kWh\)
Số tiền cần phải trả trong 30 ngày:
\(99.14000=1386000\left(đ\right)\)
òm thì môn Lí mình cx khá non nên nếu có sai bạn đừng trách mình nha![]()

a. \(Q_{thu}=mc\Delta t=2\cdot4200\cdot80=672000\left(J\right)\)
b. \(H=\dfrac{Q_{thu}}{Q_{toa}}100\%\Rightarrow Q_{toa}=\dfrac{Q_{thu}}{H}100\%=\dfrac{672000}{90}100\%\approx746666,6667\left(J\right)\)
c. \(Q_{toa}=A=Pt\Rightarrow t=\dfrac{Q_{toa}}{P}=\dfrac{746666,6667}{1000}\approx746,7\left(s\right)\)
Nhiệt lượng cần cung cấp để làm đun sôi nước:
\(Q=mc\Delta t=2\cdot4200\cdot\left(100-20\right)=672000J\)
Với hiệu suất của bếp là 90% thì nhiệt lượng bếp tỏa:
\(Q_{tp}=\dfrac{Q}{H}=\dfrac{672000}{90\%}=746666,67J\)
Thời gian cần đun sôi nước:
\(t=\dfrac{A}{P}=\dfrac{Q_{tp}}{P}=\dfrac{\dfrac{2240000}{3}}{1000}=\dfrac{2240}{3}\approx746,67s\)

a) Nhiệt lượng mà bếp tỏa ra trong 1s là Q = I2Rt = 2,52.80.1 = 500 J.
(Cũng có thể nói công suất tỏa nhiệt của bếp là P = 500W).
b) Nhiệt lượng mà bếp tỏa ra trong 20 phút là Qtp = Q.20.60 = 600000 J.
Nhiệt lượng cần để đun sôi lượng nước đã cho là
Qi = cm(t2 – t1) = 4200.1,5.(100-25) = 472500 J
Hiệu suất của bếp là: H = = 78,75 %.
c) Lượng điện năng mà bếp tiêu thụ trong 30 ngày (theo đơn vị kW.h) là:
A = Pt = 500.30.3 = 45000 W.h = 45 kW.h
Tiền điện phải trả là: T = 45.700 = 315000 đồng

Đáp án: C
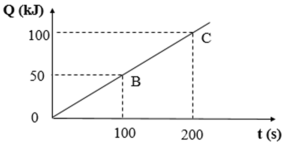
- Ta thấy cứ 100s thì nhiệt lượng bếp cung cấp được là 50kJ. Hay trong 1s bếp cung cấp được nhiệt lượng là 0,5kJ.
- Nhiệt lượng nước nhận vào để tăng nhiệt độ lên đến 100 0 C là:
Q = mc. ∆ t = 2.4200.(100 – 20) = 672000 (J) = 672 (kJ)
- Thời gian để đun sôi là:
672 : 0,5 = 1344 (s) = 22,4 (phút)