Giúp mình với mình đg cần gấp 🥺

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1 I'm not really interested in robotics.
2 We might go to the moon for our summer holiday in 2050.
3 I couldn't email you last night because my computer didn't work.
4 I didn't need to finish my homework yesterday.
5 She has worked at the school canteen for two months.
6 If you don't study hard, you won't pass the exam.




\(\left(x^2-1\right)'=2x;\left[\left(x-2\right)^4\right]'=4\cdot\left(x-2\right)^3\cdot\left(x-2\right)'=4\left(x-2\right)^3\)
\(f''\left(x\right)=\left(x^2-1\right)'\left(x-2\right)^4+\left(x^2-1\right)\left[\left(x-2\right)^4\right]'\)
\(=2x\left(x-2\right)^4+\left(x^2-1\right)\cdot4\left(x-2\right)^3\)
\(=2\left(x-2\right)^3\left[x\left(x-2\right)+2x^2-2\right]\)
\(=2\left(x-2\right)^3\left(3x^2-2x-2\right)\)
Đặt \(f'\left(x\right)=0\)
=>\(\left[{}\begin{matrix}x=1\\x=-1\\x=2\end{matrix}\right.\)
\(f''\left(2\right)=0;f''\left(1\right)=2>0;f''\left(-1\right)=-162< 0\)
=>Chọn B


a: Xét ΔAFD vuông tại F và ΔCEB vuông tại E có
AD=CB
góc FAD=góc ECB
=>ΔAFD=ΔCEB
=>DF=EB
Xét tứ giác DFBE có
DF//BE
DF=BE
=>DFBE là hình bình hành
b: S CAB=S CAD
=>CH*AB=CK*AD
=>CH*AB=CK*BC
=>CH/BC=CK/AB
Xét ΔCHK và ΔBCA có
CH/BC=CK/BA
góc HCK=góc CBA
Do đó: ΔCHK đồng dạng với ΔBCA

refer
1 . Electricity will be brought to remote areas by the government next year
2 . The problem of energy shortage will be solved by using solar energy
3 . A new hydropower plant will be built to meet the increasing demand by the government
4 . In the coming decades , renewable energy will be used everyday /
5 . Will all the world's oil be used up in the next 100 years ?
6 . Solar panels will be placed on the roofs of houses to produce hot water and electricity
7 . Cold , oil , and gas won't be replaced by alternative energy sources anytime soon
8 . Will fossil fuels be completely replaced by renewable energy in the future ?
1 . Electricity will be brought to remote areas by the government next year
2 . The problem of energy shortage will be solved by using solar energy
3 . A new hydropower plant will be built to meet the increasing demand by the government
4 . In the coming decades , renewable energy will be used everyday /
5 . Will all the world's oil be used up in the next 100 years ?
6 . Solar panels will be placed on the roofs of houses to produce hot water and electricity
7 . Cold , oil , and gas won't be replaced by alternative energy sources anytime soon
8 . Will fossil fuels be completely replaced by renewable energy in the future ?



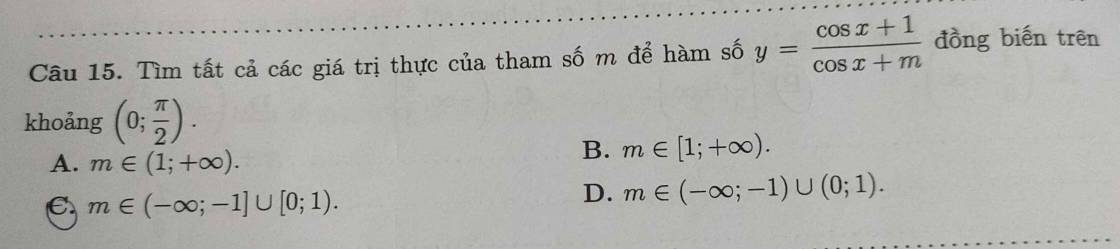




câu 1:Hai nhân vật trên vi phạm phương châm về chất.Đặc điểm nhận biết đó chính là qua lời nói của hai người,nói không đúng sự thật,không có chứng cứ xác thực
câu 2:a) Câu ấy vi phạm phương châm về lượng vì bồ câu thì đương nhiên là loài chim có hai cánh nên không cần nói có hai cánh người đọc cũng tự hiểu được
b) Phương châm lịch sự (mk ko chắc nữa)