Bài 4: Hãy chứng tỏ a // b bằng nhiều cách. A B a b 2 1 1 2 120 0 ...
Đọc tiếp
Bài 4: Hãy chứng tỏ a // b bằng nhiều cách.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
8 tháng 11 2021
Bài 2: ta thấy A và B ở vị trí trong cùng phía , A + B = 180 độ =>a//b(1)
Ta lại thấy B , C ở vị trí đồng vị , B=C=70 độ =>b//c(2)
Từ 1,2 =>a//b//c
7 tháng 6 2016
18/31 giữ nguyên . 181818/313131=18 nhân 10101/31 nhân 10101 = 18/31
18/31=181818/313131
28 tháng 10 2023
1:
\(A=\left\{0;1;2;4\right\};B=\left\{0;2;3;5;7\right\}\)
\(A\cap B=\left\{0;2\right\}\)
\(A\cup B=\left\{0;1;2;4;3;5;7\right\}\)
\(A\text{B}=\left\{1;4\right\}\)
\(B\text{A}=\left\{3;5;7\right\}\)
2: \(A\text{B}=\left\{1;4\right\}\)
\(A=\left\{0;1;2;4\right\}\)
=>(A\B)\(\subset\)A
A\(A\B)
={0;1;2;4}\{1;4}
={0;2}
=\(A\cap B\)
29 tháng 10 2016
Bài 1:
\(0,0\left(8\right)=\frac{1}{10}\cdot0,\left(8\right)=\frac{1}{10}\cdot0,\left(1\right)\cdot8=\frac{4}{5}\cdot\frac{1}{9}=\frac{4}{45}\)
\(0,1\left(2\right)=0,1+0,0\left(2\right)=\frac{1}{10}+\frac{1}{10}\cdot0,\left(2\right)=\frac{1}{10}+\frac{1}{10}\cdot0,\left(1\right)\cdot2=\frac{1}{10}+\frac{1}{5}\cdot\frac{1}{9}=\frac{1}{10}+\frac{1}{45}=\frac{11}{90}\)
\(0,1\left(23\right)=0,1+0,\left(23\right)=\frac{1}{10}+0,\left(01\right)\cdot23=\frac{1}{10}+\frac{1}{99}\cdot23=\frac{1}{10}+\frac{23}{99}=\frac{329}{990}\)
15 tháng 9 2019
Bài 1 :
Vì: a>2 => a=2+m
b>2 => b=2+n (m, n thuộc N*)
=> a+b= (2+m) +(2+n)
a.b= (2+m). (2+n)
= 2(2+n)+ m(2+n)
= 4+ 2n+ 2m+ mn
= 4+ m+ m+ n+ n+ mn
= (4+ m+ n) +(m +n +mn)
= (2+ m) +(2+ n) + (m+ n+ mn) > (2+ m)+ (2+n)
=> a.b > a+b .dpcm
~ Hok tốt ~
KY
15 tháng 9 2019
1)\(\hept{\begin{cases}a>2\\b>2\end{cases}}\Rightarrow\hept{\begin{cases}\frac{1}{a}< \frac{1}{2}\\\frac{1}{b}< \frac{1}{2}\end{cases}}\)
\(\Leftrightarrow\frac{1}{a}+\frac{1}{b}< 1\Leftrightarrow\frac{a+b}{ab}< 1\Leftrightarrow a+b< ab\)
2) \(\left(a-b\right)^2\ge0\)
\(\Leftrightarrow a^2-2ab+b^2\ge0\)
\(\Leftrightarrow a^2+b^2\ge2ab\)
\(\Leftrightarrow\frac{a^2}{ab}+\frac{b^2}{ab}\ge2\)
\(\Leftrightarrow\frac{1}{a}+\frac{1}{b}\ge2\left(đpcm\right)\)
KK
6 tháng 9 2021
C1: Ta có: A2 = 180o - 120o = 60o
Ta thấy: B1 = A2 = 60o
=> a//b (so le trong)
C2: Ta có: A2 = 60o như cách 1.
Ta có: B2 = 180o - 60o = 120o
Ta thấy: B2 + A2 = 120o + 60o = 180o
=> a//b (2 góc trong cùng phía)
C3: ta có: B2 = 120o như cách 2.
Ta thấy: B2 = A2 = 120o
=> a//b (đồng vị)
6 tháng 9 2021
\(\widehat{A_2}=180^0-120^0=60^0\)
Ta có: \(\widehat{A_2}=\widehat{B_1}\)
mà hai góc này là hai góc ở vị trí so le trong
nên a//b
LN
4
22 tháng 7 2021
2 góc so le trong bằng nhau, 2 góc so le ngoài bằng nhau, 2 góc đồng vị bằng nhau, 2 góc trong cùng phía cộng vào bằng 180o
GC
22 tháng 7 2021
- Nếu có một cặp góc so le trong bằng nhau hoặc một cặp góc đồng vị bằng nhau thì a // b.
- Nếu cặp góc trong cùng phía bù nhau.
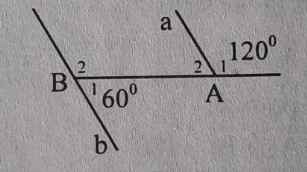
a//b
\(\widehat{B2}=\widehat{A1}\) (đồng vị)
\(\widehat{B1}=\widehat{A2}\) (so le trong)