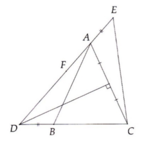
Cho tam giác ABC cân tại A ( góc A < 90 độ ). Đường trung trực cạnh AC cắt tia CB tại D. Trên tia đối của tia AD lấy điểm E sao cho AE=BD. Chứng minh:
a, Tam giác ADC cân
b, góc DAC = góc ABC
c, AD = CE
d, Lấy F là trung điểm DE. Chứng minh CF là đường trung trực của DE
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan

30 tháng 3 2022
a: Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường trung trực
b: Xét ΔDAC có
D nằm trên đường trung trực của AC
Do đó: ΔDAC cân tại D
=>\(\widehat{DAC}=\widehat{ACB}=\widehat{ABC}\)

18 tháng 5 2022
a: Ta có ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường trung trực của BC
b: Xét ΔDAC có DA=DC
nên ΔDAC cân tại D
=>\(\widehat{DAC}=\widehat{C}=\widehat{ABC}\)