Giúp em giải bài tập này vs ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(1,\\ a,=6x^4y^4-x^3y^3+\dfrac{1}{2}x^4y^2\\ b,=4x^3+5x^2-8x^2-10x+12x+15\\ =4x^3-3x^2+2x+15\\ 2,\\ a,=7\left(x^2-6x+9\right)=7\left(x-3\right)^2\\ b,=\left(x-y\right)^2-36=\left(x-y-6\right)\left(x-y+6\right)\\ 3,\\ \Leftrightarrow x\left(x^2-0,36\right)=0\\ \Leftrightarrow x\left(x-0,6\right)\left(x+0,6\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=0,6\\x=-0,6\end{matrix}\right.\)


\(b,\) Với giá trị đã tim được ở câu a, ta tiếp tục làm câu b
\(A-\dfrac{2}{\sqrt{3}}=\dfrac{\sqrt{x}}{\sqrt{x}-2}-\dfrac{2}{\sqrt{3}}\)\(\left(1\right)\)
Thay \(x=7+4\sqrt{3}\) vào \(\left(1\right)\)
\(\Rightarrow\dfrac{\sqrt{7+4\sqrt{3}}}{\sqrt{7+4\sqrt{3}}-2}-\dfrac{2}{\sqrt{3}}\)
\(=1\)


a.
$x^3-x^2-6x=0$
$\Leftrightarrow x(x^2-x-6)=0$
$\Leftrightarrow x[x(x+2)-3(x+2)]=0$
$\Leftrightarrow x(x+2)(x-3)=0$
$\Leftrightarrow x=0$ hoặc $x+2=0$ hoặc $x-3=0$
$\Leftrightarrow x=0$ hoặc $x=-2$ hoặc $x=3$
Vì $x\in\mathbb{N}^*$ nên $x=3$
Vậy $A=\left\{3\right\}$
------------------------------
b.
$(x^2-x\sqrt{3})(3x^2+5x-2)=0$
$\Leftrightarrow x(x-\sqrt{3})[x(3x-1)+2(3x-1)]=0$
$\Leftrightarrow x(x-\sqrt{3})(3x-1)(x+2)=0$
$\Leftrightarrow x=0$ hoặc $x-\sqrt{3}=0$ hoặc $3x-1=0$ hoặc $x+2=0$
$\Leftrightarrow x\in\left\{0; \sqrt{3}; \frac{1}{3}; -2\right\}$
Vì $x\in\mathbb{Q}$ nên $x\in\left\{0; \frac{1}{3}; -2\right\}$
Vậy $B=\left\{0; \frac{1}{3}; -2\right\}$
c.
$(x-5)^2=49$
$\Leftrightarrow (x-5)^2=7^2=(-7)^2$
$\Leftrightarrow x-5=7$ hoặc $x-5=-7$
$\Leftrightarrow x=12$ hoặc $x=-2$
$x\in\mathbb{N}$ nên $x=12$
Vậy $C=\left\{12\right\}$
-------------------------------
d.
$|x|<5\Leftrightarrow -5< x< 5$
$x\in\mathbb{Z}\Rightarrow x\in\left\{-4; -3; -2; -1; 0; 1; 2;3;4\right\}$
Mà $x^2>5$ nên $x\in\left\{-4; -3; 3; 4\right\}$
Vậy $D=\left\{-4; -3; 3; 4\right\}$

a) \(\widehat{AED}=\widehat{AFD}=90^o\) nên \(E,F\) cùng nhìn \(AD\) dưới góc vuông suy ra \(AEDF\) nội tiếp.
suy ra \(\widehat{AEF}=\widehat{ADF}\).
mà \(\widehat{ADF}=\widehat{ACD}\) (vì cùng phụ với góc \(\widehat{DAC}\))
suy ra \(\widehat{AEF}=\widehat{ACD}\Rightarrow\widehat{BEF}+\widehat{FCB}=180^o\) suy ra \(BEFC\) nội tiếp.
b) \(\Delta GBE\sim\Delta GFC\left(g.g\right)\)
suy ra \(GB.GC=GE.GF\).
\(\Delta GDE\sim\Delta GFD\left(g.g\right)\)
suy ra \(GD^2=GE.GF\).
\(ACBH\) nội tiếp suy ra \(GB.GC=GH.GA\)
suy ra \(GD^2=GH.GA\)
\(\Rightarrow\Delta GHD\sim\Delta GDA\left(c.g.c\right)\)
\(\Rightarrow\widehat{GHD}=\widehat{GDA}=90^o\)
suy ra \(DH\) vuông góc với \(AG\).


 ai giải giúp em mấy bài toán này vs ạ giải chi tiết giúp em ạ
ai giải giúp em mấy bài toán này vs ạ giải chi tiết giúp em ạ

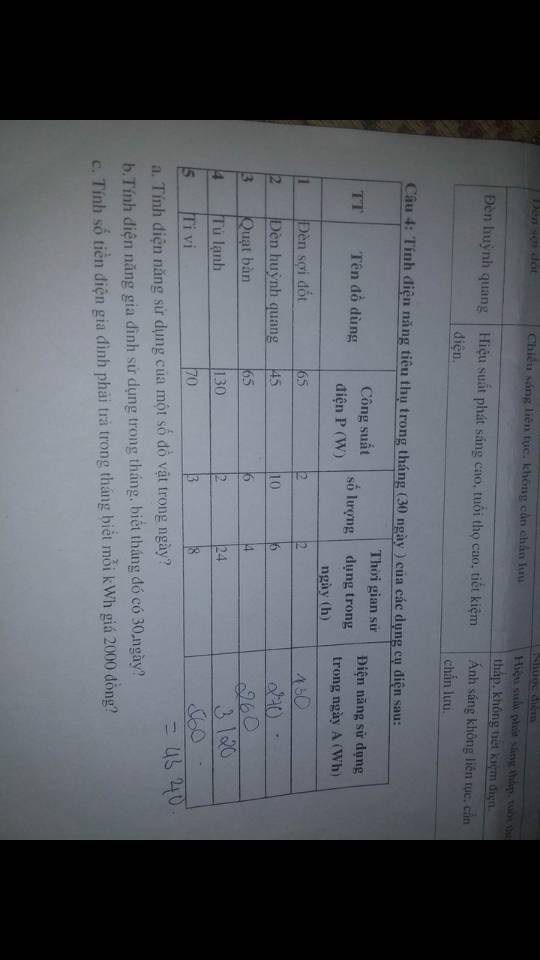


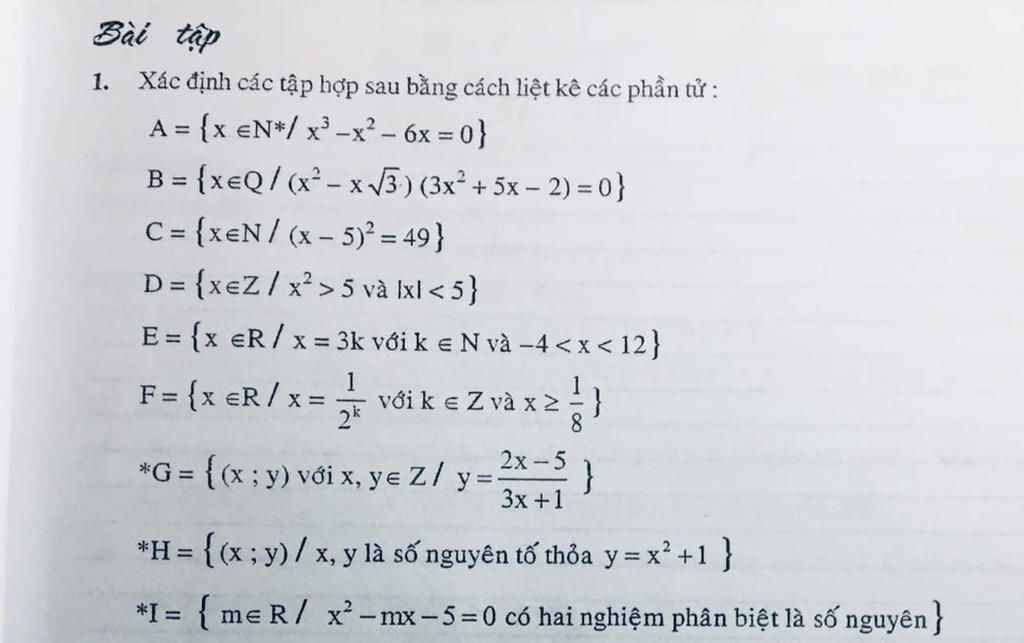
 Giúp em giải bài tập này với ạ. Em cảm ơn.
Giúp em giải bài tập này với ạ. Em cảm ơn.

