cho a3+8b3 = 1 - 6ab. tính a+2b
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 7 2021
\(a;b>0\Rightarrow3a+2b+1>1\)
\(\Rightarrow log_{3a+2b+1}\left(9a^2+b^2+1\right)\) đồng biến
Mà \(9a^2+b^2\ge2\sqrt{9a^2b^2}=6ab\Rightarrow log_{3a+2b+1}\left(9a^2+b^2+1\right)\ge log_{3a+2b+1}\left(6ab+1\right)\)
\(\Rightarrow log_{3a+2b+1}\left(9a^2+b^2+1\right)+log_{6ab+1}\left(3a+2b+1\right)\ge log_{3a+2b+1}\left(6ab+1\right)+log_{6ab+1}\left(3a+2b+1\right)\ge2\)
Đẳng thức xảy ra khi và chỉ khi: \(\left\{{}\begin{matrix}log_{6ab+1}\left(3a+2b+1\right)=1\\3a=b\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}6ab+1=3a+2b+1\\b=3a\end{matrix}\right.\)
\(\Rightarrow18a^2+1=3a+6a+1\)
\(\Leftrightarrow18a^2-9a=0\Rightarrow\left\{{}\begin{matrix}a=\dfrac{1}{2}\\b=\dfrac{3}{2}\end{matrix}\right.\)
15 tháng 10 2023
\(P=2a^3+2b^3+6ab-2024\)
\(=2\left[\left(a+b\right)^3-3ab\left(a+b\right)\right]+6ab-2024\)
\(=2\left[1-3ab\left(a+b\right)\right]+6ab-2024\)
\(=2-6ab+6ab-2024\)
=-2022
15 tháng 10 2023
cái khúc dấu bằng thứ 2 và thứ 3, sao biến đổi mấy số trong ngoặc thành -6ab ạ
28 tháng 9 2021
\(=\left(\dfrac{2}{3}a\right)^3-3.\left(\dfrac{2}{3}\right)^2a^2.2b+3.\dfrac{2}{3}a.4b^2-\left(2b\right)^3=\left(\dfrac{2}{3}a-2b\right)^3\)
HA
0
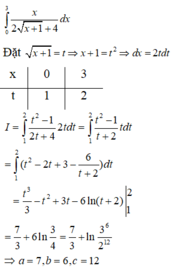
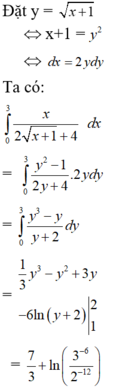
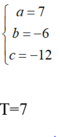
Lời giải:
\(a^3+8b^3=1-6b\)
\(\Leftrightarrow a^3+8b^3+6ab-1=0\)
\(\Leftrightarrow (a+2b)^3-3.a.2b(a+2b)+6ab-1=0\)
\(\Leftrightarrow [(a+2b)^3-1]-6ab(a+2b-1)=0\)
\(\Leftrightarrow (a+2b-1)[(a+2b)^2+(a+2b)+1]-6ab(a+2b-1)=0\)
\(\Leftrightarrow (a+2b-1)(a^2+4b^2+1+a+2b-2ab)=0\)
\(\Rightarrow \left[\begin{matrix} a+2b-1=0(1)\\ a^2+4b^2+1+a+2b-2ab=0(2)\end{matrix}\right.\)
Với \((1)\Rightarrow a+2b=1\)
Với \((2)\Rightarrow 2a^2+8b^2+2+2a+4b-4ab=0\)
\(\Leftrightarrow (a^2+4b^2-4ab)+(a^2+2a+1)+(4b^2+4b+1)=0\)
\(\Leftrightarrow (a-2b)^2+(a+1)^2+(2b+1)^2=0\)
\(\Rightarrow (a-2b)^2=(a+1)^2=(2b+1)^2=0\)
\(\Rightarrow \left\{\begin{matrix} a=-1\\ 2b=-1\end{matrix}\right.\Rightarrow a+2b=-2\)
Vậy $a+2b\in \left\{1;-2\right\}
Lời giải:
\(a^3+8b^3=1-6b\)
\(\Leftrightarrow a^3+8b^3+6ab-1=0\)
\(\Leftrightarrow (a+2b)^3-3.a.2b(a+2b)+6ab-1=0\)
\(\Leftrightarrow [(a+2b)^3-1]-6ab(a+2b-1)=0\)
\(\Leftrightarrow (a+2b-1)[(a+2b)^2+(a+2b)+1]-6ab(a+2b-1)=0\)
\(\Leftrightarrow (a+2b-1)(a^2+4b^2+1+a+2b-2ab)=0\)
\(\Rightarrow \left[\begin{matrix} a+2b-1=0(1)\\ a^2+4b^2+1+a+2b-2ab=0(2)\end{matrix}\right.\)
Với \((1)\Rightarrow a+2b=1\)
Với \((2)\Rightarrow 2a^2+8b^2+2+2a+4b-4ab=0\)
\(\Leftrightarrow (a^2+4b^2-4ab)+(a^2+2a+1)+(4b^2+4b+1)=0\)
\(\Leftrightarrow (a-2b)^2+(a+1)^2+(2b+1)^2=0\)
\(\Rightarrow (a-2b)^2=(a+1)^2=(2b+1)^2=0\)
\(\Rightarrow \left\{\begin{matrix} a=-1\\ 2b=-1\end{matrix}\right.\Rightarrow a+2b=-2\)
Vậy $a+2b\in \left\{1;-2\right\}$