Một vật dao động điều hòa có biên độ A = 4cm, gia tốc của vật tại vị trí biên có độ lớn 400cm/s2. Tốc độ góc là
A. 10rar/s. B. 20rad/s. C. 15rad/s. D. 5rad/s.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Δt là khoảng thời gian giữa hai lần liên tiếp vật có động năng bằng thế năng => ∆ t = T 4
Theo đề bài ta có: ![]()
Công thức độc lập với thời gian giữa gia tốc và vận tốc:
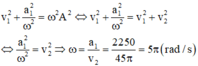
Thay vào công thức tính được biên độ dao động A = 6 3 cm

Đáp án C
+ Khoảng thời gian 2 lần liên tiếp có động năng bằng thế năng là
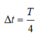
+ Tại thời điểm t1 ta có:
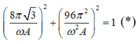
+ Sau đó 1 khoảng thời gian
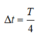
nên v1 vuông pha với v2
![]()
+ Thay vào (*) ta tìm được 1 khoảng thời gian
![]()

- Vận tốc ở vị trí thấp nhất là vận tốc cực đại:
\(v_{max}=\omega.A=\sqrt{\dfrac{g}{l}}.\alpha.l=\sqrt{gl}\alpha\)
- Gia tốc ở vị trí cao nhất (ở biên)
\(a_{max}=\omega^2.A=\dfrac{g}{l}.\alpha.l=g.\alpha\)
\(\Rightarrow \alpha=\dfrac{a_{max}}{g}=1/10(rad)\)
\(\Rightarrow \alpha=5,73^0\)
P.S: Không cần dùng đến giả thiết vận tốc ở vị trí thấp nhất.
Vật ở vị trí biên : \(\Leftrightarrow a=\omega^2A\Leftrightarrow\omega=\sqrt{\dfrac{a}{A}}=10\left(rad\backslash s\right)\)