Mọi người giúp tui với :333
Tìm một số có hai chữ số, nếu chia số đó cho tổng hai chữ số được thương là 6. Nếu cộng tích hai chữ số với 25 thì được số nghịch đảo.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
9 tháng 2 2019
goi so co hai chu so co dang la \(\overline{ab}\) ( 0<a<10,b<9: a,b la so tu nhien ）
Theo de bai ta co : \(\overline{ab}\): (a+b) =6
\(\Leftrightarrow\overline{ab}=6a+6b\)
\(\Leftrightarrow10a+b=6a+6b\)
\(\Leftrightarrow4a=5b\)
\(\Leftrightarrow a=\dfrac{5}{4}b\left(1\right)\)
Ta lai co : \(a\times b+25=\dfrac{1}{\overline{ab}}\)
\(\Leftrightarrow\overline{ab}\times\left(ab+25\right)=1\)
\(\Leftrightarrow ab\left(10a+b\right)+25=1\)
Tu (1) ta dc : \(\dfrac{5}{4}b\times b\left(10\times\dfrac{5}{4}b+b\right)+25=1\)
N
24 tháng 1 2019
Gọi 2 chữ số của số đó là a và b. ĐK: a,b \(\in\) N*.
Ta có hpt: \(\left\{{}\begin{matrix}10a+b=6\left(a+b\right)\left(1\right)\\ab+25=10b+a\left(2\right)\end{matrix}\right.\)
Từ (1)=>\(4a-5b=0\Leftrightarrow b=\dfrac{4a}{5}\)
\(\left(2\right)\Leftrightarrow9a-\dfrac{4a^2}{5}-25=0\)
\(\Leftrightarrow\left[{}\begin{matrix}a=\dfrac{25}{4}\left(KTM\right)\\a=5\left(TM\right)\end{matrix}\right.\)
\(\Rightarrow b=4\)
Vậy số đó là 54. Đúng không vậy thầy?
CM
28 tháng 5 2019
Gọi a là chữ số hàng chục, b là chữ số hàng đơn vị. Điều kiện a, b nguyên 1 ≤ a ≤ 9 và 0 ≤ b ≤ 9. Ta có:
'
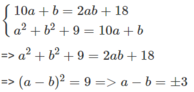Trường hợp 1
a - b = 3 ⇒ a = b + 3
Thay vào phương trình đầu của hệ phương trình ta được:
11b + 30 = 2(b + 3)b + 18 ⇒ 2 b 2 - 5 b + 12 = 0
Phương trình cuối có hai nghiệm: b 1 = 4 , b 2 = -3/2
Giá trị b 2 = -3/2 không thỏa mãn điều kiện 0 ≤ b ≤ 9 nên nên bị loại.
Vậy b = 4, suy ra a = 7.
Trường hợp 2
a - b = - 3 ⇒ a = b - 3
Thay vào phương trình của hệ phương trình ra được
11b - 30 = 2(b - 3)b + 18 ⇒ 2 b 2 - 17 b + 48 = 0
Phương trình này vô nghiệm.
Vậy số phải tìm là 74.
BT
5 tháng 5 2017
Gọi số cần tìm có dạng: \(\overline{ab}\) \(\left(a,b\in N;a,b>0\right)\)
Thương của số cần tìm với tích hai chữ số của nó có dạng:\(\overline{ab}:\left(ab\right)\).
Theo giả thiết ta có: \(\overline{ab}=2ab+18\).
Tổng bình phương các chữ số của số cần tìm là: \(a^2+b^2+9=\overline{ab}\).
Ta có hệ phương trình: \(\left\{{}\begin{matrix}2ab+18=\overline{ab}\\a^2+b^2+9=\overline{ab}\end{matrix}\right.\)\(\Rightarrow a^2+b^2+9=2ab+18\)\(\Leftrightarrow\left(a-b\right)^2=9\)\(\Leftrightarrow\left|a-b\right|=3\).
Th 1. \(a-b=3\)\(\Leftrightarrow a=b+3\). Khi đó:
\(2ab+18=\overline{ab}\)\(\Leftrightarrow2ab+18=10a+b\)\(\Leftrightarrow2\left(b+3\right)b+18=10\left(b+3\right)+b\)\(\Leftrightarrow2b^2-5b-12=0\)\(\Leftrightarrow\left\{{}\begin{matrix}b=4\left(tm\right)\\b=\dfrac{-3}{2}\left(l\right)\end{matrix}\right.\).
Với \(b=4\) ta có \(a=3+b=3+4=7\). Vậy số đó là 73.
Th2: \(a-b=-3\)\(\Leftrightarrow a=b-3\). Khi đó:
\(2ab+18=10a+b\)\(\Leftrightarrow2\left(b-3\right)b+18=10\left(b-3\right)+b\)
\(\Leftrightarrow2b^2-17b+48=0\) (Vô nghiệm).
Vậy số cần tìm là: 73.
29 tháng 6 2023
Gọi số cần tìm là \(\overline{ab}\)
Theo đề, ta có: a+b=9 và ab+25=10b+a
=>b=9-a và a(9-a)+25=10(9-a)+a
=>9a-a^2+25=90-10a+a
=>-9a+90=-a^2+9a+25
=>a^2-18a+65=0
=>a=5(nhận) hoặc a=13(loại)
=>Số cần tìm là 54
LM
7 tháng 4 2020
Gọi số có 2 chữ số cần tìm là: ab \(\left(a,b\inℕ^∗;a,b\le9\right)\)
Theo bài ra, ta có hệ phương trình: \(\hept{\begin{cases}\overline{ab}
=6\left(a+b\right)\\\overline{ba}
=a.b+25\end{cases}
\Leftrightarrow\hept{\begin{cases}10a+b=6a+6b\\10b+a=ab+25\end{cases}
}}\)
\(\Leftrightarrow\hept{\begin{cases}4a=5b\\10b+a=a.b+25\end{cases}}
\Leftrightarrow\hept{\begin{cases}b=\frac{4a}{5}\\9a=\frac{4a^2}{5}+25\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}b=\frac{4a}{5}\\4a^2-45a+125=0\end{cases}
\Leftrightarrow\hept{\begin{cases}b=\frac{4a}{5}\\\orbr{\begin{cases}a=5\\a=\frac{25}{4}
\left(loai\right)\end{cases}}\end{cases}}}
\Leftrightarrow\hept{\begin{cases}a=5\\b=4\end{cases}
}\)Vậy: số cần tìm là 54.
LM
7 tháng 4 2020
Ôi :(( Bạn tự giải nốt hệ phương trình và loại nghiệm phân số đi nhé :(( Không hiểu sao của mình bị mất 2 bước cuối :(( Xin lỗi bạn
Gọi số cần tìm là ab thì theo mô tả teong đề ra, ta có : \(\hept{\begin{cases}\overline{ab}=\left(a+b\right).6\\a.b+25=\overline{ba}\end{cases}}\Leftrightarrow\hept{\begin{cases}10.a+b=6a+6b\\a.b+25=10b+a\end{cases}\Leftrightarrow..}\)
\(\hept{\begin{cases}4a=5b\\\left(b-1\right)\left(10-a\right)=15\end{cases}\Leftrightarrow\hept{\begin{cases}a=5\\b=4\end{cases}.}}\) ĐÁP SỐ Số cần tìm là : \(\overline{ab}=54\)
(Trong bài ra : Nếu cộng tích hai số đó với 25 thì được số NGHỊCH ĐẢO , Ta hiểu : Được số có hai chữ số VIẾT NGƯỢC LẠI số đã cho.Số đã cho là ab thì viết ngược lại là ba )