Question

[Cao Viết Cường]

1, Đặt vật sáng AB có độ cao h, vuông góc với trục chính của TKHT có tiêu cự f, điểm A nằm trên trục chính, cách thấu kính ột khoảng d. Ảnh A'B' của vật AB có độ cao h' và hứng trên màn cách thấu kính khoảng d'

a, chứng minh rằng độ phóng đại ảnh k = \(\frac{A'B'}{AB}=\frac{h'}{h}=\frac{d'}{d}\)

b, chứng minh mối liên hệ giữa tiêu cự thấu kính, khoảng cách từ vật đén thấu kính và khoảng cách từ ảnh đến thấu kính tuân theo biểu thức \(\frac{1}{f}=\frac{1}{d}+\frac{1}{d'}\)

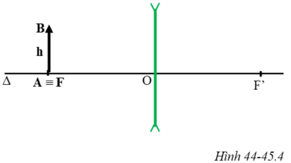
2, Đặt vật sáng AB cao 2cm, vuông góc với trục chính của TKHT có tiêu cự 10cm, điểm B nằm trên trục chính , cách thấu kính 15cm

a, Vẽ ảnh A'B' của vật AB theo tỉ xích tùy chọn

b, Tính khoảng cách từ ánh đến thấu kính và chiều cao của ảnh A'B'

c, Nếu dịch chuyển vật AB ra xa thấu kính thêm 10cm thì chiều cao của ảnh A'B' thay đổi thế nào? Ảnh A'B' có hứng trên màn chắn không

d, Nếu dịch chuyển vật AB lại gần thấu kính thêm 10cm thì chiều cao của ảnh A'B' thay đổi thế nào? Ảnh A'B' có hứng trên màn chắn không

Answer 1

[Nhung Hoàng]

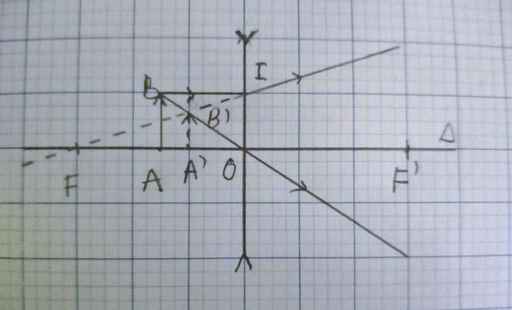
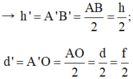
1) a) ta có : OAB đồng dạng OA'B' ( g.g)

=> OA/OA'= AB/A'B'

=> OA'/OA= AB/A'B' => d'/d=h'/h

b) ta có : AB/A'B' = OA/OA' ( CMT)

=> AB/A'B'= d/d' (*)

ta có: OIF' đồng dạng A'B'F' ( g.g)

=> OI/A'B'= OF/A'F'

MÀ OI = AB ; A'F' = OA'-OF' = d-f

=> AB/A'B' = f/d'-f ( **)

từ (*) và (**) ta có:

d/d' = f/d'-f

<=> d.( d' - f) = d'.f

<=> d.d'-d.f= d'.f ( ***)

Chia 2 vế của ( ***) cho d.d'.f

ta có : 1/f - 1/d' = 1/d

<=> 1/f = 1/d + 1/d'