Cho tam giác DEG có M là trung điểm DE, MN//DG N thuộc EG
a.chứng minh N là trung điểm EG ?
b.cho MN=5cm . Tính DG ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
26 tháng 9 2021
a: Xét ΔDEG có
H là trung điểm của EG
HK//DG
Do đó: K là trung điểm của DE
Xét ΔDEG có
H là trung điểm của EG
K là trung điểm của DE
Do đó: HK là đường trung bình của ΔDEG
14 tháng 6 2020
tự kẻ hình nghen:33333
a) vì AD cắt BE tại G mà AD, BE là hai đường trung tuyến=> G là trọng tâm của tam giác ABC
=> EG=1/3BE, BG=2/3BE
=> GD=1/3AD, AG=2/3AD
=> EG+EN=2*1/3BE (GE=EN)=> GN=2/3BE=> GN=BG=2/3BE
=> GD+DM=2*1/3AD (GD=DM)=> GM=2/3AD=> GM=AG=2/3AD
b) xét tam giác AGB và tam giác MGN có
GN=BG(cmt)
GM=AG(cmt)
AGB=MGN( đối đỉnh)
tam giác AGB=tam giác MGN (cgc)
MN=AB( hai cạnh tương ứng)
=> BAG=GMN( hai góc tương ứng)
mà BAG so le trong với GMN=> AB//MN
NH
1
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
8 tháng 7 2023
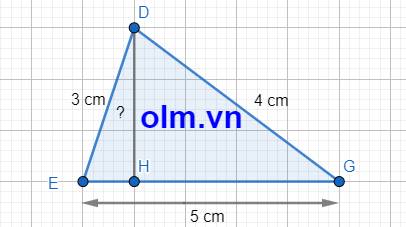
Gọi độ dài cạnh EH là \(x\) (cm); 0 < \(x< 5\)
Độ dài cạnh HG là: 5 - \(x\) (cm)
Xét tam giác vuông HDE vuông tại H, theo pytago ta có:
DH2 = 32 - \(x^2\) = 9 - \(x^2\)(1)
Xét tam giác vuông DHG vuông tại H theo pytago ta có:
DH2 = 42 - (5 - \(x\))2 = -\(x^2\) + 10\(x\) - 9(2)
Từ (1) và (2) ta có:
-\(x^2\) + 10\(x\) - 9 = 9 - \(x^2\)
10\(x\) = 18
\(x\) = 1,8 (thỏa mãn)
Thay \(x\) = 1,8 vào biểu thức (1) ta có:
DH2 = 9 - (1,8)2 = 5,76
DH = \(\sqrt{5,76}\) = 2,4 (cm)
Kết luận: độ dài đoạn DH là 2,4 cm
24 tháng 3 2020
Kham khảo nha , tớ ko chắc về cái CM : AK = CG =BI của mk
a,Xét \(\Delta\)AEK và \(\Delta\) CEG có:
EA=EC(gt)
EG=EK(gt)
^AEK = ^GEC( 2 góc đối đỉnh)
=> \(\Delta\)AEK = \(\Delta\)CEG(c.g.c)
=> AK = GC
cm tương tự ta có: \(\Delta\)GDC = \(\Delta\)IDB(c.g.c)
=> GC=BI và AK=GC => AK=GC=B
b, Theo câu a, ta có \(\Delta\)AEK = \(\Delta\)CEG(c.g.c)
=> ^EAK = ^ECG
=> AK//GC
theo câu a, ta có: \(\Delta\)GDC=\(\Delta\)IDB(c.g.c)
=> ^DGC= ^DIB=> GC//BI và AK//GC
=> AK//BI
c, ta có: AD là đường trung tuyến ứng với cạnh BC của \(\Delta\)ABC
BE là đường trung tuyến ứng với cạnh AC của \(\Delta\)ABC
=> giao của AD và BE là trọng tâm của \(\Delta\)ABC
=> G là trọng tâm của \(\Delta\)ABC
=> GA = 2GD
mà GI = ID
=> GA = GI + ID = GI
ta có G là trọng tâm của \(\Delta\)ABC; BE là đường trung tuyến của \(\Delta\)ABC
=> BG = 2GE mà GE = EK
=> BG = GE + EK = GK
xét \(\Delta\)GAK và \(\Delta\)GIB có :
GA=GI(cmt)
GK=GB(cmt)
^AGK= ^BGI(2 góc đối đỉnh)
=>\(\Delta\)GAK=\(\Delta\)GIB(c.g.c)
3 tháng 10 2021
a) Xét tam giác MNP có:
D là trung điểm MN
DE//NP
E thuộc MP
=> E là trung điểm MP
b) Xét tam giác MNP có:
D là trung điểm MN
E là trung điểm MP
=> DE là đường trung bình
\(\Rightarrow DE=\dfrac{1}{2}NP=\dfrac{1}{2}.6=3\left(cm\right)\)
a) Xét tam giác DEG có:
M là trung điểm DE(gt)
MN//DG(gt)
=> N là trung điểm EG
b) Xét tam giác DEG có:
M là trung điểm DE(gt)
N là trung điểm EG(cmt)
=> MN là đường trung bình
\(\Rightarrow DG=2MN=2.5=10\left(cm\right)\)