Giúp mk với sáng t2 mk phải nộp r thanks 😊
Bài 1 a, vẽ đồ thị hàm số y=1.5x^2
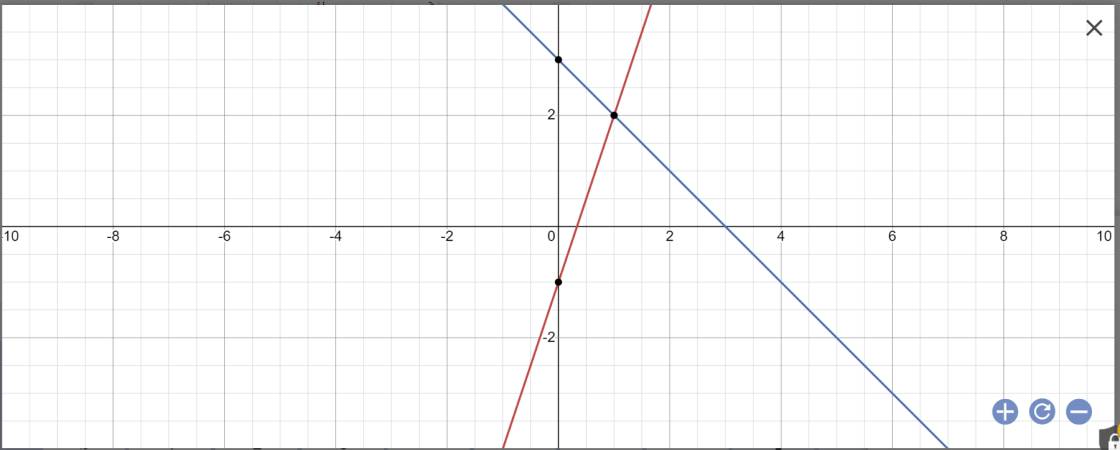
b, tìm tọa độ giao điểm của đồ thị y=01.5x^2 với y=0.5x +1 . Gọi A, B là giao điểm 2 đồ thị trên . Tính SΔAOB
Bài 2 Cho phương trình x^2+2(m-2)x-2m+1=0
Chứng minh rằng phương trình luôn có 2 nghiệm phân biệt với mọi giá trị của m. Tìm m để phương trình có 2 nghiệm cùng dương