Cho hình bình hành ABCD co BC=2AB mà A=60 độ
Gọi Evà F là trung điểm của BC và AD
a)Tứ giác ECDF;ABED là hình gì? vì sao?
b)Tính số đo góc A;E;D?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
4 tháng 9 2022
a: Xét tứ giác ABEF có
BE//AF
BE=AF
Do đó: ABEF là hình bình hành
mà BE=BA
nên ABEF là hình thoi
b: Xét ΔBEI có BE=BI
nên ΔBEI cân tại B
mà góc IBE=60 độ
nên ΔBEI đều
=>góc EIB=60 độ
=>góc EIA=góc IAF
=>AIEF là hình thang cân
c: Xét ΔABD có
BF là đườ trung tuyến
BF=AD/2
D đó: ΔBAD vuông tại B
=>góc IBD=90 độ
Xét tứ giác BICD có
BI//CD
BI=CD
DO đó: BICD là hình bình hành
mà góc IBD=90 độ
nên BICD là hình chữ nhật
3 tháng 12 2021
a: Xét ΔABC có
E là trung điểm của BC
F là trung điểm của AC
Do đó: EF là đường trung bình của ΔABC
Suy ra: EF//AD và EF=AD
Xét tứ giác ADEF có
EF//AD
EF=AD
Do đó: ADEF là hình bình hành
mà \(\widehat{FAD}=90^0\)
nên ADEF là hình chữ nhật
mà AD=AF
nên ADEF là hình vuông
7 tháng 11 2015
BẠN TỰ VẼ HÌNH NHÉ MÌNH GIẢI THÔI NHA ^^
Giải
a) Xét tam giác ODE, có:
IK là đường trung bình(I t/điểm OD và K trung điểm OE)
=>IK // DE
Vậy:IKED là hình thang
b) Ta có IAKO là hcn (A=AIO=AKO=90 độ)
=>AK=IO và AK // IO.
Mà D,I,O thẳng hàng và DI=IO (D đxứng O qua I)
=>AK//DI và AK=DI
=>AKDI là hbh.
c)Ta có tam giác ABC có góc A=90 độ và Góc C=30 độ
=>góc B=60 độ
Và tam giác ABC vuông ở A và AM là đường trung tuyến
=> AM =1/2 BC =>AM=BM
=>Tam giác ABM cân ở M. Và Góc B= 60độ (cmt)
=> Tam giác ABM đều => AB=AM=BM
Vậy chu vi tam giác ABC= 3 x 7=21 (cm)
2 tháng 11 2021
a: Xét tứ giác DCEF có
DF//EC
DF=EC
Do đó: DCEF là hình bình hành
KV
10 tháng 11 2023
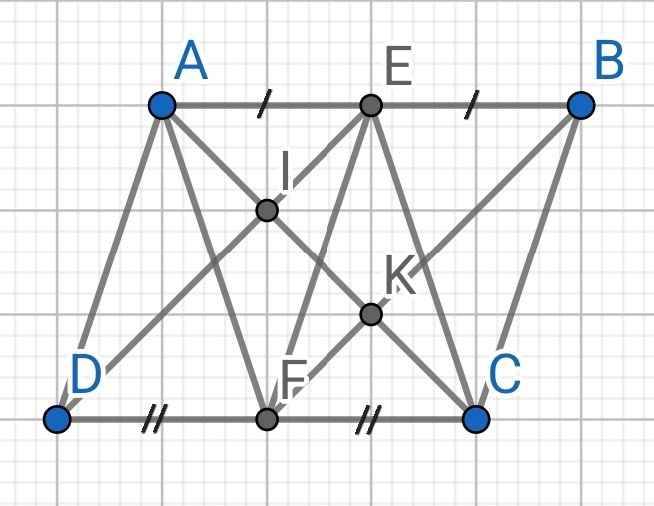a) Do ABCD là hình bình hành (gt)
⇒ AB = CD (1)
Do E là trung điểm AB (gt)
⇒ AE = BE = AB : 2 (2)
Do F là trung điểm CD (gt)
⇒ CF = DF = CD : 2 (3)
Từ (1), (2) và (3)
⇒ AE = BE = CF = DF
Do ABCD là hình bình hành (gt)
⇒ AB // CD
⇒ AE // CF
Tứ giác AECF có:
AE // CF (cmt)
AE = CF (cmt)
⇒ AECF là hình bình hành
b) Do AB // CD (cmt)
⇒ BE // DF
Tứ giác BEDF có:
BE // DF (cmt)
BE = DF (cmt)
⇒ BEDF là hình bình hành
⇒ BF // DE
⇒ BK // EI và KF // DI
∆CDI có:
F là trung điểm CD (gt)
KF // DI (cmt)
⇒ K là trung điểm của CI
⇒ CK = IK (4)
∆ABK có:
E là trung điểm của AB (gt)
BK // EI (cmt)
⇒ I là trung điểm của AK
⇒ AI = IK (5)
Từ (4) và (5)
⇒ AI = IK = KC
11 tháng 3 2020
a, xét tứ giác BICG có :
M là trung điểm cuả BC do AM là trung tuyến (gt)
M là trung điểm của GI do I đx G qua M (gt)
=> BICG là hình bình hành (dh)
+ G là trọng tâm của tam giác ABC (gt)
=> GM = AG/2 và GN = BG/2 (đl)
E; F lần lượt là trung điểm của GB; GA (gt) => FG = AG/2 và GE = BG/2 (tc)
=> FG = GM và GN = GE
=> G là trung điểm của FM và EN
=> MNFE là hình bình hành (dh)
b, MNFE là hình bình hành (câu a)
để MNFE là hình chữ nhật
<=> NE = FM
có : NE = 2/3BN và FM = 2/3AM
<=> AM = BN mà AM và BN là trung tuyến của tam giác ABC (Gt)
<=> tam giác ABC cân tại C (đl)
c, khi BICG là hình thoi
=> BG = CG
BG và AG là trung tuyến => CG là trung tuyến
=> tam giác ABC cân tại A