giải phương trình
(x2+10)2 - 13(x2+10) + 22=0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
2 tháng 5 2022
a) Khi \(m=1\) thì pt đã cho trở thành \(x^2-2x-10=0\) (*)
pt (*) có \(\Delta'=\left(-1\right)^2-\left(-10\right)=11>0\)
Do đó (*) có 2 nghiệm phân biệt \(\left[{}\begin{matrix}x_1=\dfrac{-\left(-1\right)+\sqrt{11}}{1}=1+\sqrt{11}\\x_2=\dfrac{-\left(-1\right)-\sqrt{11}}{1}=1-\sqrt{11}\end{matrix}\right.\)
b) Xét pt đã cho \(x^2-mx-10=0\) \(\left(a=1;b=-m;c=-10\right)\)
Nhận thấy \(ac=1\left(-10\right)=-10< 0\) nên pt đã cho luôn có 2 nghiệm phân biệt \(x_1,x_2\).
Áp dụng hệ thức Vi-ét, ta có \(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{-m}{1}=m\\x_1x_2=\dfrac{-10}{1}=-10\end{matrix}\right.\)
Ta có \(x_1^2+x_2^2=29\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=29\Leftrightarrow m^2-2\left(-10\right)=29\)\(\Leftrightarrow m^2+20=29\Leftrightarrow m^2=9\Leftrightarrow m=\pm3\)
Vậy để pt đã cho có 2 nghiệm phân biệt thỏa mãn đề bài thì \(m=\pm3\)
CM
17 tháng 1 2019
Đặt m = 2 x 2 +x -2
Ta có: 2 x 2 + x - 2 2 +10 x 2 +5x -16 =0
⇔ 2 x 2 + x - 2 2 +5(2 x 2 +x -2) -6 =0
⇔ m 2 +5m -6 =0
Phương trình m 2 +5m -6 = 0 có hệ số a = 1, b = 5, c = -6 nên có dạng
a + b + c = 0
Suy ra : m 1 =1 , m 2 =-6
m1 =1 ta có: 2 x 2 +x -2 =1 ⇔ 2 x 2 +x -3=0
Phương trình 2 x 2 +x -3 = 0 có hệ số a = 2, b = 1 , c = -3 nên có dạng
a +b+c=0
Suy ra: x 1 =1 , x 2 =-3/2
Với m=-6 ta có: 2 x 2 +x -2 = -6 ⇔ 2 x 2 +x +4 =0
∆ = 1 2 -4.2.4 = 1 -32 = -31 < 0 . Phương trình vô nghiệm
Vậy phương trình đã cho có 2 nghiệm : x 1 =1 , x 2 =-32
PT
1
28 tháng 2 2021
4) Ta có: \(\dfrac{2x-5}{5}-\dfrac{x+3}{3}=\dfrac{2-3x}{2}-x-2\)
\(\Leftrightarrow\dfrac{6\left(2x-5\right)}{30}-\dfrac{10\left(x+3\right)}{30}=\dfrac{15\left(2-3x\right)}{30}-\dfrac{30\left(x+2\right)}{30}\)
\(\Leftrightarrow12x-30-10x-30=30-45x-30x-60\)
\(\Leftrightarrow-22x-60=-75x-30\)
\(\Leftrightarrow-22x+75x=-30+60\)
\(\Leftrightarrow53x=30\)
\(\Leftrightarrow x=\dfrac{30}{53}\)
Vậy: \(S=\left\{\dfrac{30}{53}\right\}\)
5) Ta có: \(\dfrac{5x-3}{6}-\dfrac{7x-1}{4}=5\)
\(\Leftrightarrow\dfrac{2\left(5x-3\right)}{12}-\dfrac{3\left(7x-1\right)}{12}=\dfrac{60}{12}\)
\(\Leftrightarrow10x-6-21x+3=60\)
\(\Leftrightarrow-11x-3=60\)
\(\Leftrightarrow-11x=63\)
\(\Leftrightarrow x=-\dfrac{63}{11}\)
Vậy: \(S=\left\{-\dfrac{63}{11}\right\}\)
28 tháng 2 2021
`9,x^3+x^2-2=0`
`x^3-x^2+2x^2-2=0`
`<=>x^2(x-1)+2(x-1)(x+1)=0`
`<=>(x-1)(x^2+2x+2)=0`
`<=>x=1`
`14,x^2-2x+1=0`
`<=>(x-1)^2=0`
`<=>x-1=0`
`<=>x=1`
`15,x^3+3x^2+3x+1=0`
`<=>(x+1)^3=0`
`<=>x+1=0`
`<=>x=-1`
CM
20 tháng 11 2019
a)
3 · x 2 + x 2 - 2 x 2 + x - 1 = 0 ( 1 )
Đặt t = x 2 + x ,
Khi đó (1) trở thành : 3 t 2 – 2 t – 1 = 0 ( 2 )
Giải (2) : Có a = 3 ; b = -2 ; c = -1
⇒ a + b + c = 0
⇒ (2) có hai nghiệm t 1 = 1 ; t 2 = c / a = - 1 / 3 .
+ Với t = 1 ⇒ x 2 + x = 1 ⇔ x 2 + x – 1 = 0 ( * )
Có a = 1; b = 1; c = -1 ⇒ Δ = 1 2 – 4 . 1 . ( - 1 ) = 5 > 0
(*) có hai nghiệm
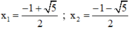
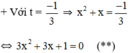
Có a = 3; b = 3; c = 1 ⇒ Δ = 3 2 – 4 . 3 . 1 = - 3 < 0
⇒ (**) vô nghiệm.
Vậy phương trình (1) có tập nghiệm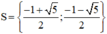 
b)
x 2 − 4 x + 2 2 + x 2 − 4 x − 4 = 0 ⇔ x 2 − 4 x + 2 2 + x 2 − 4 x + 2 − 6 = 0 ( 1 )
Đặt x 2 – 4 x + 2 = t ,
Khi đó (1) trở thành: t 2 + t – 6 = 0 ( 2 )
Giải (2): Có a = 1; b = 1; c = -6
⇒ Δ = 1 2 – 4 . 1 . ( - 6 ) = 25 > 0
⇒ (2) có hai nghiệm
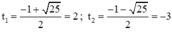
+ Với t = 2 ⇒ x 2 – 4 x + 2 = 2
⇔ x 2 – 4 x = 0
⇔ x(x – 4) = 0
⇔ x = 0 hoặc x = 4.
+ Với t = -3 ⇒ x 2 – 4 x + 2 = - 3
⇔ x2 – 4x + 5 = 0 (*)
Có a = 1; b = -4; c = 5 ⇒ Δ ’ = ( - 2 ) 2 – 1 . 5 = - 1 < 0
⇒ (*) vô nghiệm.
Vậy phương trình ban đầu có tập nghiệm S = {0; 4}.
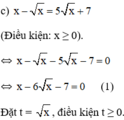
Khi đó (1) trở thành: t 2 – 6 t – 7 = 0 ( 2 )
Giải (2): Có a = 1; b = -6; c = -7
⇒ a – b + c = 0
⇒ (2) có nghiệm t 1 = - 1 ; t 2 = - c / a = 7 .
Đối chiếu điều kiện chỉ có nghiệm t = 7 thỏa mãn.
+ Với t = 7 ⇒ √x = 7 ⇔ x = 49 (thỏa mãn).
Vậy phương trình đã cho có nghiệm x = 49.
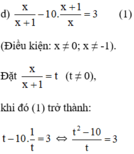
⇔ t 2 – 10 = 3 t ⇔ t 2 – 3 t – 10 = 0 ( 2 )
Giải (2): Có a = 1; b = -3; c = -10
⇒ Δ = ( - 3 ) 2 - 4 . 1 . ( - 10 ) = 49 > 0
⇒ (2) có hai nghiệm:
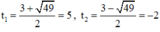
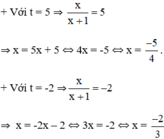
Cả hai nghiệm đều thỏa mãn điều kiện xác định.
Vậy phương trình đã cho có tập nghiệm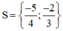 
28 tháng 2 2021
Bài 6:
1) Ta có: \(2x\left(x-5\right)-\left(x+3\right)^2=3x-x\left(5-x\right)\)
\(\Leftrightarrow2x^2-10x-\left(x^2+6x+9\right)=3x-5x+x^2\)
\(\Leftrightarrow2x^2-10x-x^2-6x-9-3x+5x-x^2=0\)
\(\Leftrightarrow-14x-9=0\)
\(\Leftrightarrow-14x=9\)
\(\Leftrightarrow x=-\dfrac{9}{14}\)
Vậy: \(S=\left\{-\dfrac{9}{14}\right\}\)
28 tháng 2 2021
`1)2x(x-5)-(x+3)^2=3x-x(5-x)`
`<=>2x^2-10x-x^2-6x-9=3x-5x+x^2`
`<=>x^2-16x-9=x^2-2x`
`<=>14x=-9`
`<=>x=-9/14`
PT
1
CM
5 tháng 1 2020
b) 2 x 2 + x + 10 = 0
Ta có: a = 2; b = 1; c = 10
Δ = b 2 - 4ac = 1 2 - 4.2.10 = -79 < 0
⇒ Phương trình đã cho vô nghiệm.
CM
29 tháng 6 2019
Đáp án D
T a c ó : - 10 x 2 + 40 = 0 ⇔ - 10 x 2 = - 40 ⇔ x 2 = 4 ⇔ x = ± 2
Đặt \(x^2+10=t\)
\(\Rightarrow t^2-13t+22=0\)
\(\Leftrightarrow t^2-11t-2t+22=0\)
\(\Leftrightarrow t\left(t-11\right)-2\left(t-11\right)=0\)
\(\Leftrightarrow\left(t-11\right)\left(t-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}t-2=0\\t-11=0\end{matrix}\right.\)
Tự làm nốt