Cho hai đường thẳng (d1): y=mx+m và (d2): \(y=\frac{-1}{m}x+\frac{1}{m}\). Gọi I(x0;y0) là giao điểm của hai đường thẳng đó. Tính \(T=x0^2+y0^2\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
10 tháng 5 2021
Lời giải:
Giao điểm của 2 đường thẳng thuộc trục hoành nên có dạng $(a,0)$. Vì điểm này thuộc $(d_1):x+y=-1$ nên $a+0=-1\Rightarrow a=-1$
Vậy giao điểm của 2 ĐT trên là $(-1,0)$
Giao điểm này $\in (d_2)$ khi mà $m.(-1)+0=1$
$\Leftrightarrow m=-1$
5 tháng 4 2020
Giải
Đường thẳng( d1 ) : y = -mx + m + 1 có a1 = -m
Đường thẳng ( d2 ) : y =\(\frac{1}{m}x-1-\frac{5}{m}\)có a2 = \(\frac{1}{m}\)
Ta có : a1.a2 = ( -m ) . \(\frac{1}{m}\)=-1 .Vậy ( d1 ) và ( d2 ) vuông góc với nhau với mọi giá trị của tham số m khác 0 => đpcm
CM
20 tháng 4 2018
Với m = 2 thì d 1 : y = 2x + 3; d 2 : y = x + 1
Tập xác định của hàm số R
Bảng giá trị
| x | 0 | - 1 |
| y = 2x + 3 | 3 | 1 |
| x | 0 | - 1 |
| y = x + 1 | 1 | 0 |
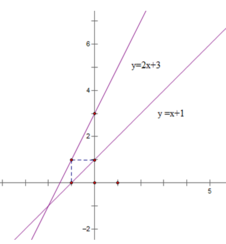
Gọi A ( x 0 ; y 0 ) là tọa độ giao điểm của d1 và d2
Khi đó:
( y 0 = 2 x 0 + 3 và y 0 = x 0 + 1
⇒ 2xo + 3 = x 0 + 1 ⇔ x 0 = -2
⇒ y 0 = x 0 + 1 = -2 + 1 = -1
Vậy tọa độ giao điểm của d 1 và d 2 là (-2; -1)
28 tháng 2 2017
a)
\(\left(d1\right):y=mx+m-3=m\left(x+1\right)-3\Rightarrow\left\{\begin{matrix}x=-1\\y=-3\end{matrix}\right.\) với mọi m:
ĐIểm cố dịnh là A(-1,-3)
\(\left(d1\right):y=\dfrac{1}{m}x+\dfrac{1-m}{m}=\dfrac{1}{m}\left(x+1\right)-1\Rightarrow voi..x=-1...thi...y=-1...voi..\forall m\ne0\)
ĐIểm cố định B(-1,-1)
10 tháng 3 2022
\(d_1:mx+y=3m-1.\\ \Leftrightarrow-mx+3m-1=y.\)
\(d_2:x+my=m+1.\\ \Leftrightarrow my=-x+m+1.\\\Leftrightarrow y=\dfrac{-x}{m}+\dfrac{m}{m}+\dfrac{1}{m}.\Leftrightarrow y=-\dfrac{1}{m}x+1+\dfrac{1}{m}.\)
Thay m = 2 vào phương trình đường thẳng d1 ta có:
\(-2x+3.2-1=y.\\ \Leftrightarrow-2x+5=y.\)
Thay m = 2 vào phương trình đường thẳng d2 ta có:
\(y=-\dfrac{1}{2}x+1+\dfrac{1}{2}.\\ \Leftrightarrow y=\dfrac{-1}{2}x+\dfrac{3}{2}.\)
Xét phương trình hoành độ giao điểm của d1 và d2 ta có:
\(-2x+5=\dfrac{-1}{2}x+\dfrac{3}{2}.\\ \Leftrightarrow\dfrac{-3}{2}x=-\dfrac{7}{2}.\\ \Leftrightarrow x=\dfrac{7}{3}.\)
\(\Rightarrow y=\dfrac{1}{3}.\)
Tọa độ giao điểm của d1 và d2 khi m = 2 là \(\left(\dfrac{7}{3};\dfrac{1}{3}\right).\)
23 tháng 10 2021
b: Phương trình hoành độ giao điểm là:
x+1=-x+3
\(\Leftrightarrow2x=2\)
\(\Leftrightarrow x=1\)
hay y=2
Phương trình hoành độ giao điểm:
\(mx_0+m=\dfrac{-1}{m}x_0+\dfrac{1}{m}\) (ĐK: \(m\ne0\))
\(m^2x_0+m^2=-x_0+1\)
\(x_0\left(m^2+1\right)=1-m^2\)
\(x_0=\dfrac{1-m^2}{m^2+1}\) (1)
Mà theo (d1): \(y_0=mx_0+m\)
Suy ra: \(y_0=m.\dfrac{1-m^2}{m^2+1}+m\)
\(y_0=\dfrac{m-m^3+m^3+m}{m^2+1}\)
\(y_0=\dfrac{2m}{m^2+1}\) (2)
Thế (1) và (2) vào T ta được:
\(T=\left(\dfrac{1-m^2}{m^2+1}\right)^2+\left(\dfrac{2m}{m^2+1}\right)^2\)
\(T=\dfrac{m^4-2m^2+1+4m^2}{m^4+2m^2+1}\)
\(T=1\)