Cho hai điểm A,B cố định phân biệt nằm cùng phía với đường thẳng d. Tìm trên đường thẳng d điểm C để tam giác ABC có chu vi nhỏ nhất. Em cảm ơn trước.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
8 tháng 4 2017
Lấy A’’ đối xứng với A qua d.
Chu vi tam giác ABC = AB + AC + BC = AB + CA’’+ CB
Vì độ dài AB không đổi nên để chu vi tam giác ABC nhỏ nhất khi và chỉ khi CA” + CB nhỏ nhất.
Lại có; C A " + C B ≥ A " B
Do đó, để chu vi tam giác ABC nhỏ nhất khi và chỉ khi CA” + CB = A”B. Khi đó: B, C, A’’ thẳng hàng.
Đáp án C
13 tháng 7 2018
EM MỚI HỌC LỚP 6 , EM CHƯA BÍT BÀI NÀY THÔNG CẢM NHA !!!
CM
19 tháng 12 2019
. Gọi A' là điểm đối xứng của A qua d Þ A' cố định.
Vì C Î d Þ CA = CA' (tính chất đối xứng trục). Ta có:
PDABC = AB + AC + BC
= AB + (CA' + CB) ≥ AB + BA' (không đổi. Dấu "=" xảy ra tức là chu vi tam giác nhỏ nhất khi C là giao điểm của d và BA'
28 tháng 5 2015
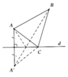
- Tìm điểm A’ đối xứng với A qua d
- Nối A’B cắt d tại M . M chính là điểm cần tìm .
- Thật vậy : Vì A’ đối xứng với A qua d cho nên MA=MA’ (1). Do đó :
MA+MB=MA’+MB=A’B .
- Giả sử tồn tại M’ khác M thuộc d thì : M’A+M’B=M’A’+M’B
'A B≥
. Dấu bằng chỉ
xảy ra khi A’M’B thẳng hàng . Nghĩa là M trùng với M’
21 tháng 2 2023
1: Điểm cố định của (d) là:
x=0 và y=m*0+2=2
2: PTHĐGĐ là:
x2-mx-2=0
a=1; b=-m; c=-2
Vì a*c<0
nên (P) luôn cắt (d) tại hai điểm khác phía so với trục tung