Cho hình vuông ABCD có độ dài cạnh bằng 12 cm. Trên cạnh AB lấy E sao cho BE=3cm. Đường thẳng DE cắt cạnh CB kéo dài tại K
a) Tính DE
b) Chứng minh tam giác EAD đồng dạng với tam giác EBK, tính tỉ số đồng dạng k
c) Chứng minh AD2 = KC. AE
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

bạn ơi hình như bạn ghi lộn đúng ko đoạn đường thẳng DE cach CB kéo dài tại K OQ

\
a) Xét tam giác EAD và tam giác EBK có :
\(\widehat{EAD}=\widehat{EBK}\left(=90^o\right)\)
\(\widehat{AED}=\widehat{KEB}\left(đđ\right)\)
\(\Rightarrow\) Tam giác EAD đồng dạng với tam giác EBK ( g-g ) ( đpcm )
b) Do tam giác EAD đồng dạng với tam giác EBK ( chứng minh ở câu a )
\(\Rightarrow\widehat{EKB}=\widehat{EDA}\)
Xét tam giác ADE và tam giác CKD có :
\(\widehat{EKB}=\widehat{EDA}\)
\(\widehat{EAD}=\widehat{KCD}\left(=90^o\right)\)
\(\Rightarrow\) Tam giác ADE đồng dạng với tam giác CKD ( g-g )
\(\Rightarrow\frac{AD}{AE}=\frac{KC}{CD}\) (1)
Mà CD = AD ( đều là cạnh của hình vuông ABCD ) (2)
Từ (1) và (2) :
\(\Rightarrow\frac{AD}{AE}=\frac{KC}{AD}\)
\(\Leftrightarrow AD^2=KC\times AE\left(đpcm\right)\)
c) Ta có : AB = 8 cm
Mà ABCD là hình vuông nên AB = BC = CD = AD = 8 cm
Theo giả thiết : \(BE=\frac{1}{4}AB\Rightarrow BE=2\left(cm\right)\)
\(\Rightarrow AE=AB-BE=8-2=6\left(cm\right)\)
Theo câu b , ta có : \(AD^2=KC\times AE\)
\(\Rightarrow8^2=KC\times6\)
\(\Leftrightarrow KC=\frac{32}{3}\left(cm\right)\)
Ta có :
\(S_{CDK}=\frac{CD\times CK}{2}=\frac{8\times\frac{32}{3}}{2}=\frac{128}{3}\left(cm^2\right)\)
Vậy khi độ dài AB = 8 cm thì \(S_{CDK}=\frac{128}{3}cm^2\)

i don't now
mong thông cảm !
...........................

a) Áp dụng định lí: Một đường thẳng cắt hai cạnh của tam giác và song song với cạnh còn lại tạo thành một tam giác mới đồng dạng với tam giác đã cho.
ΔFCD có EB // CD (E ∈ FD, B ∈ FC)
⇒ ΔFEB 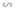 ΔFDC (1)
ΔFDC (1)
ΔAED có FB // AD (F ∈ DE, B ∈ AE)
⇒ ΔFEB 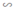 ΔDEA (2)
ΔDEA (2)
Từ (1) và (2) suy ra: ΔDEA 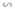 ΔFDC (tính chất)
ΔFDC (tính chất)
b) AB = 12cm, AE = 8cm
⇒ EB = AB – AE = 12 - 8 = 4cm.
Vì ABCD là hình bình hành nên AD = BC = 7cm
Do ΔFEB 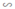 ΔDEA
ΔDEA
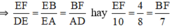
⇒ EF = 5cm, BF = 3,5cm.

a) Áp dụng định lí: Một đường thẳng cắt hai cạnh của tam giác và song song với cạnh còn lại tạo thành một tam giác mới đồng dạng với tam giác đã cho.
ΔFCD có EB // CD (E ∈ FD, B ∈ FC)
⇒ ΔFEB  ΔFDC (1)
ΔFDC (1)
ΔAED có FB // AD (F ∈ DE, B ∈ AE)
⇒ ΔFEB  ΔDEA (2)
ΔDEA (2)
Từ (1) và (2) suy ra: ΔDEA  ΔFDC (tính chất)
ΔFDC (tính chất)
b) AB = 12cm, AE = 8cm
⇒ EB = AB – AE = 12 - 8 = 4cm.
Vì ABCD là hình bình hành nên AD = BC = 7cm
Do ΔFEB 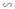 ΔDEA
ΔDEA
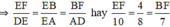
⇒ EF = 5cm, BF = 3,5cm.

a: Xet ΔEAD và ΔEBF có
góc EAD=góc EBF
góc AED=góc BEF
=>ΔEAD đồng dạng với ΔEBF
=>AD/BF=EA/EB
=>18/BF=9/6=3/2
=>BF=12cm

a) Ta có: AE+EB=AB(E nằm giữa A và B)
nên AE=AB-EB=12-3=9(cm)
Áp dụng định lí Pytago vào ΔAED vuông tại A, ta được:
\(DE^2=AD^2+AE^2\)
\(\Leftrightarrow DE^2=12^2+9^2=225\)
hay DE=15(cm)
Vậy: DE=15cm