Cho tam giác nhọn ABC có chân đường cao hạ từ A,B,C là O(0;0) \(I\left(\dfrac{8}{5};\dfrac{24}{5}\right)\) J(-2;6). Viets phương trình ba chạn của tam giác ABC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
4 tháng 8 2019
A B C M N D E
Ta có ^MEN = ^NBD + ^MCD = 1800 - ^MAN. Suy ra tứ giác AMEN nội tiếp
Cũng dễ có tứ giác BCMN nội tiếp đường tròn (BC)
Từ đó ^AEM = ^ANM = ^MCB = ^MCD = 1800 - ^MED. Hay ^AEM + ^MED = 1800
Vậy thì A,E,D thẳng hàng (đpcm).
KN
27 tháng 2 2020
Ta có ^BCN = ^BMN ( do tứ giác BNMC nội tiếp )
=> ^NBC = ^AMN ( cùng phụ với hai góc bằng nhau ) (1)
Mặt khác do BDEN và CDEM là các tứ giác nội tiếp chung cạnh DE
Nên ^NBD + ^MCD = ^NEM ( tính chất góc ngoài tứ giác nội tiếp )
Mà ^NBD + ^MCD + ^NAM = 1800
Suy ra ^NEM + ^NAM = 1800 . Vây AMEN nội tiếp
Do đó: ^AMN = ^AEN (2)
Từ (1) và (2) suy ra ^NBD = ^AEN
Mà ^NBD + ^DEN = 1800 (do BDEN nội tiếp)
Nên ^DEN + ^AEN = 1800 => ^AED=1800 .
Vậy ba điểm A, E, D thẳng hàng (đpcm)
18 tháng 5 2021
d:x+y-2=0 A B C I E(3;1) D(-2;1) P(2;1)
Ta dễ có tứ giác ABDE nội tiếp đường tròn đường kính AB => ^CDE = ^BAE
Lại có ^BAE = ^CAD (= 900 - ^ACB), suy ra ^CDE = ^CAD = 900 - ^ACD => DE vuông góc AC
Thấy D,E,P cùng có tung độ bằng 1 => D,E,P thẳng hàng, vì P thuộc AC nên DE vuông góc với AC tại P
Đường thẳng AC: đi qua P(2;1), VTPT \(\overrightarrow{DE}=\left(5;0\right)\) \(\Rightarrow AC:x-2=0\)
Xét hệ: \(\hept{\begin{cases}x-2=0\\x+y-2=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=2\\y=0\end{cases}}\Rightarrow A\left(2;0\right)\)
Đường thẳng BC: đi qua \(D\left(-2;1\right)\),VTPT \(\overrightarrow{DA}=\left(4;-1\right)\Rightarrow BC:4x-y+9=0\)
Xét hệ: \(\hept{\begin{cases}x-2=0\\4x-y+9=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=2\\y=17\end{cases}\Rightarrow C\left(2;17\right)}\)
Đường thẳng BE: đi qua \(E\left(3;1\right)\), VTPT \(\overrightarrow{AE}=\left(1;1\right)\Rightarrow BE:x+y-4=0\)
Xét hệ: \(\hept{\begin{cases}4x-y+9=0\\x+y-4=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=-1\\y=5\end{cases}}\Rightarrow B\left(-1;5\right)\)
Vậy \(A\left(2;0\right),B\left(-1;5\right),C\left(2;17\right)\).
12 tháng 5 2023
a: Xét ΔBDA vuông tại D và ΔBFC vuông tại F co
góc B chung
=>ΔBDA đồng dạng vói ΔBFC
b: góc BFC=góc BEC=90 độ
=>BFEC nội tiếp
=>góc AFE=góc ACB
=>ΔAFE đồng dạng vói ΔACB
c: Xét ΔAEH vuông tại E và ΔADC vuông tại D có
góc EAH chung
=>ΔAEH đồng dạng vói ΔADC
=>AD*AH=AE*AC
Xét ΔCEH vuông tại E và ΔCFA vuông tại F có
góc ECH chung
=>ΔCEH đồng dạng vói ΔCFA
=>CH*CF=CE*CA
=>AH*AD+CH*CF=CA^2
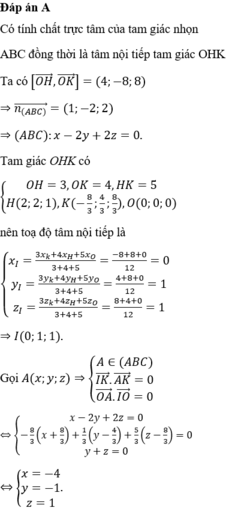
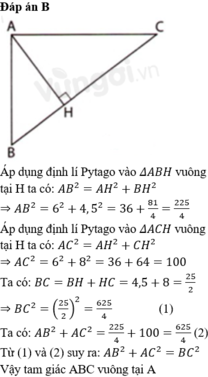
A B C O I J H
Ta có tứ giác OCIH nội tiếp (O và I đều nhìn CH dưới 1 góc vuông)
\(\Rightarrow\widehat{AOI}=\widehat{ACJ}\) (góc nội tiếp cùng chắn cung IH)
Lại có tứ giác ACOJ nội tiếp (O và J cùng nhìn AC dưới 1 góc vuông)
\(\Rightarrow\widehat{AOJ}=\widehat{ACJ}\) (góc nội tiếp cùng chắn cung AJ)
\(\Rightarrow\widehat{AOI}=\widehat{AOJ}\Rightarrow OA\) là phân giác của \(\widehat{IOJ}\)
Chứng minh tương tự ta có \(IB\) là phân giác \(\widehat{OIJ}\) ; \(JC\) là phân giác \(\widehat{IJO}\)
\(\overrightarrow{OI}=\left(\frac{8}{5};\frac{24}{5}\right)\Rightarrow\) đường thẳng OI có 1 vtpt \(\overrightarrow{n_{OI}}=\left(3;-1\right)\)
\(\Rightarrow\) pt OI: \(3x-y=0\)
Tương tự, \(\overrightarrow{n_{OJ}}=\left(3;1\right)\) \(\Rightarrow\) pt OJ: \(3x+y=0\)
Gọi \(M\left(x;y\right)\) là 1 điểm thuộc đường OA
\(\Rightarrow d\left(M;OI\right)=d\left(M;OJ\right)\Rightarrow\frac{\left|3x-y\right|}{\sqrt{3^2+\left(-1\right)^2}}=\frac{\left|3x+y\right|}{\sqrt{3^2+1^2}}\)
\(\Rightarrow\left[{}\begin{matrix}3x-y=3x+y\\y-3x=3x+y\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}y=0\\x=0\end{matrix}\right.\)
Do \(y_I\) cùng dấu \(y_J\Rightarrow I;J\) nằm cùng phía đường thẳng \(y=0\)
\(\Rightarrow\) \(y=0\) là pt đường phân giác ngoài của \(\widehat{IOJ}\) hay chính là pt đường thẳng BC
\(x=0\) là pt đường phân giác trong hay là pt đường thẳng OA
//Làm tương tự ta sẽ được pt AB và AC