Cho đường tròn (o) đường kính AB và hai điểm E , F nằm trên đg tròn . Các đường thẳng AE và BF cắt nhau tại P nằm ngoài đường tròn (o) . AF và BF cắt nhau tại Q. c/m rằng PQ vuông góc với AB
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
14 tháng 1
a: Xét tứ giác BEFC có \(\widehat{BEC}=\widehat{BFC}=90^0\)
nên BEFC là tứ giác nội tiếp đường tròn đường kính BC
=>B,E,F,C cùng thuộc một đường tròn
tâm I là trung điểm của BC
b: Xét ΔABC có
BF,CE là các đường cao
BF cắt CE tại H
Do đó: H là trực tâm của ΔABC
=>AH\(\perp\)BC
=>AM\(\perp\)BC
Xét (O) có
ΔAMD nội tiếp
AD là đường kính
Do đó: ΔAMD vuông tại M
=>AM\(\perp\)MD
Ta có: AM\(\perp\)BC
AM\(\perp\)MD
Do đó: BC//MD
Xét (O) có
\(\widehat{ABC}\) là góc nội tiếp chắn cung AC
\(\widehat{ADC}\) là góc nội tiếp chắn cung AC
Do đó: \(\widehat{ABC}=\widehat{ADC}\)
Xét (O) có
ΔACD nội tiếp
AD là đường kính
Do đó: ΔACD vuông tại C
Ta có: \(\widehat{BAH}+\widehat{ABC}=90^0\)(AH\(\perp\)BC)
\(\widehat{ADC}+\widehat{CAD}=90^0\)(ΔACD vuông tại C)
mà \(\widehat{ABC}=\widehat{ADC}\)
nên \(\widehat{BAH}=\widehat{CAD}\)
=>\(\widehat{BAH}+\widehat{MAD}=\widehat{CAD}+\widehat{MAD}\)
=>\(\widehat{BAD}=\widehat{CAM}\)(1)
Xét (O) có
\(\widehat{BAD}\) là góc nội tiếp chắn cung BD
\(\widehat{BCD}\) là góc nội tiếp chắn cung BD
Do đó: \(\widehat{BAD}=\widehat{BCD}\left(2\right)\)
Xét (O) có
\(\widehat{CBM}\) là góc nội tiếp chắn cung CM
\(\widehat{CAM}\) là góc nội tiếp chắn cung CM
Do đó: \(\widehat{CBM}=\widehat{CAM}\left(3\right)\)
Từ (1),(2),(3) suy ra \(\widehat{CBM}=\widehat{BCD}\)
Xét tứ giác BCDM có BC//DM
nên BCDM là hình thang
Hình thang BCDM có \(\widehat{CBM}=\widehat{BCD}\)
nên BCDM là hình thang cân
c: Xét (O) có
ΔABD nội tiếp
AD là đường kính
Do đó: ΔABD vuông tại B
=>BA\(\perp\)BD
mà CH\(\perp\)BA
nên CH//BD
Ta có: CD\(\perp\)CA
BH\(\perp\)AC
Do đó: BH//CD
Xét tứ giác BHCD có
BH//CD
BD//CH
Do đó: BHCD là hình bình hành
=>BC cắt HD tại trung điểm của mỗi đường
mà I là trung điểm của BC
nên I là trung điểm của HD
=>H,I,D thẳng hàng
d: Kẻ tiếp tuyến Ax của (O)
Xét (O) có
\(\widehat{xAC}\) là góc tạo bởi tiếp tuyến Ax và dây cung AC
\(\widehat{ABC}\) là góc nội tiếp chắn cung AC
Do đó: \(\widehat{xAC}=\widehat{ABC}\)
mà \(\widehat{ABC}=\widehat{AFE}\left(=180^0-\widehat{EFC}\right)\)
nên \(\widehat{xAC}=\widehat{AFE}\)
mà hai góc này là hai góc ở vị trí so le trong
nên EF//Ax
Ta có: Ax//EF
Ax\(\perp\)AD
Do đó: AD\(\perp\)EF tại K
6 tháng 2 2021
a) Xét (O) có: AB đường kính (gt), F ϵ (O)
⇒ △ BAF vuông tại F.
⇒ BF vuông góc với AF tại F. hay BF vuông góc với KF
Mà CD vuông góc với KF tại K (gt)
⇒ CD//BF
⇒ 2 cung nhỏ CF và BD chắn 2 dây // của (O) sẽ bằng nhau.
⇒ Đcpcm
b) Ta thấy CDBF là hình thang cân ( CD//BF, CF = BD )
⇒ 2 đường chéo BC = DF. (1)
Mà △ BCE cân tại B ( vì có BH vừa là đ/c, vừa là đường trung tuyến của △)
⇒BC=BE.(2)
Từ (1) và (2) ⇒ DF = BE.
⇒ cung DF = cung BE
Cộng 2 vế trên với cung EF ta đc:
cung DE = cung BF
⇒ DE = BF
CM
7 tháng 6 2019
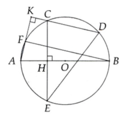
a, HS tự chứng minh
b, Từ giả thiết ta có AB là đường trung trực của CE => B C ⏜ = B E ⏜ = B F ⏜ = D E ⏜
c, Sử dụng mối liên hệ cung và dây
GN
25 tháng 3 2018
a,Xét tứ giác ACHI có: góc ACB = 90o (góc nội tiếp chắn nửa đường tròn)
góc HIA = 90o (gt)
=> tổng hai góc này =180o mà đỉnh C và I lại nằm ở vị trí đối nhau => tứ giác ACHI là tứ giác nội tiếp đường tròn đường kính AH (đpcm)
Phải là AF cắt BE tại Q ms đúng , mk ghi lầm .
Vì E, F thuộc (O) nên: \(\widehat{AEB}=\widehat{AFB}=90^o\)(Góc nội tiếp chắn nửa đường tròn).
\(\Rightarrow\)AF, BE là hai đường cao của tam giác APB.
Mà AF và BE cắt nhau tại Q. Nên Q là trực tâm của tam giác APB.
\(\Rightarrow\)PQ là đường cao thứ 3 \(\Rightarrow PQ\perp AB\left(đfcm\right)\)