Vật AB có dạng hình mũi tên từ A đến B,được đặt vuông góc với trục chính của một thấu kính hội tụ có tiêu cự f=12 cm.Điểm A cách thấu kính một khoảng bằng 24cm.Và chiều cao AB=15mm
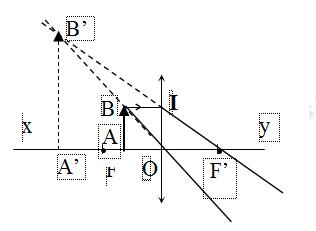
a) Dựng ảnh A’B’ của AB qua thấu kính
b) Tính khoảng cách từ ảnh tới thấu kính và chiều cao của ảnh?







Bài này không phải Toán, là Lí nhưng thấy nó khá liên quan nên mình làm luôn.
b,
Tóm tắt:
AB = h = 15 mm = 1,5 cm
OA = d = 24 cm
OF = OF' = f = 12cm
A'O = ? A'B' = ?
Bài làm:
Ta có: \(\Delta ABO~\Delta A'B'O\left(g-g\right)\)\(\Rightarrow\frac{A'B'}{AB}=\frac{A'O}{AO}\left(1\right)\)
Lại có: \(\Delta IOF'\:~\Delta B'A'F'\left(g-g\right)\Rightarrow\frac{A'B'}{OI}=\frac{A'F'}{OF'}\)
Mà AB = OI \(\Rightarrow\frac{A'B'}{AB}=\frac{A'B'}{OI}\)
\(\Rightarrow\frac{A'O}{AO}=\frac{A'F'}{OF'}=\frac{A'O-OF'}{OF'}\)
\(\Leftrightarrow\frac{A'O}{24}=\frac{A'O-12}{12}\Leftrightarrow12A'O=24A'O-288\Leftrightarrow12A'O=288\Leftrightarrow A'O=24cm\)
Thay A'O= 24cm vào (1) ta được: \(\frac{A'B'}{1,5}=\frac{24}{24}=1\Rightarrow A'B'=1,5cm\)
Vậy A'O = 24cm; A'B' = 1,5cm