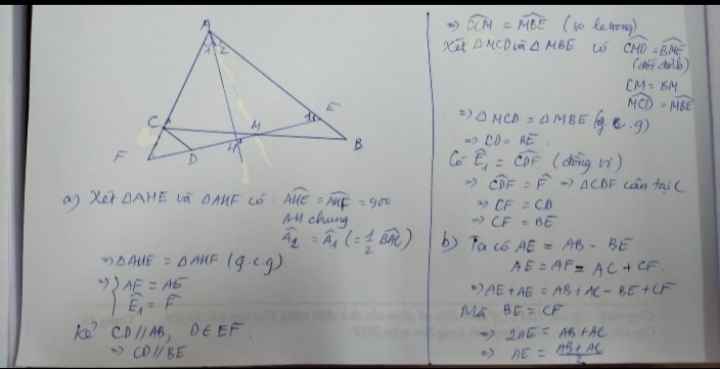
Vì BE, AE lần lượt là phân giác góc ABC và góc BAD nên ˆB1=ˆB2;ˆA1=ˆA2B1^=B^2;A1^=A^2
Xét ΔABEΔABE có ˆAEB=180∘−(ˆA1+ˆB1)AEB^=180∘−(A1^+B1^)
Suy ra ˆAEB=180∘−(ˆA2+ˆB2)AEB^=180∘−(A^2+B^2)
=360∘−(ˆA+ˆB)2=360∘−(A^+B^)2
Lại có ˆA+ˆB+ˆC+ˆD=360∘A^+B^+C^+D^=360∘ (tổng bốn góc trong tứ giác ABCD)
⇒ˆC+ˆD=3600−(ˆA+ˆB)⇒C^+D^=3600−(A^+B^)
⇒ˆAEB=ˆC+ˆD2⇒AEB^=C^+D^2
Ta có: ˆB2=ˆxBA2;ˆA2=ˆyAB2B2^=xBA^2;A2^=yAB^2 (tính chất tia phân giác)
Xét ΔABFΔABF có ˆAFB=180∘−(ˆA2+ˆB2)AFB^=180∘−(A2^+B2^)
=1800−(ˆxBA2+ˆyAB2)=3600−(ˆxBA+ˆyAB)2=3600−(1800−ˆB+1800−ˆA)2=ˆA+ˆB2=1800−(xBA^2+yAB^2)=3600−(xBA^+yAB^)2=3600−(1800−B^+1800−A^)2=A^+B^2
Vậy ˆAEB=ˆC+ˆD2AEB^=C^+D^2 và ˆAFB=ˆA+ˆB2.AFB^=A^+B^2.
Bạn tự vẽ hình nha