Cho tam giác ABC. chứng minh AB+AC>BC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
27 tháng 7 2023
a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
=>ΔAHB=ΔAHC
=>góc BAH=góc CAH
=>AH là phân giác của góc BAC
b: C ABC=10+10+12=32
AT
18 tháng 11 2016
1) Ta có hình vẽ sau:
Vì AB // CD nên \(\widehat{A_1}\) = \(\widehat{C_1}\) (so le trong)
AD // BC nên \(\widehat{A_2}\) = \(\widehat{C_2}\) ( so le trong)
Xét ΔABC và ΔCDA có:
\(\widehat{A_1}\) = \(\widehat{C_1}\) (cm trên)
AC: Cạnh chung
\(\widehat{A_2}\) = \(\widehat{C_2}\) (cm trên)
\(\Rightarrow\) ΔABC = ΔCDA (g.c.g) (đpcm)
2) Chứng minh tương tự ta có: ΔCDA = ABC (g.c.g)
\(\Rightarrow\) AB = CD ( 2 cạnh tương ứng) (đpcm)
3) Mình sửa lại chỗ AE = AC là AE = AB đó nha, bn ghi nhầm đề!!!
Ta có hình vẽ sau:
Xét ΔABC và ΔAFE có:
AE = AB (gt)
\(\widehat{A_1}\) = \(\widehat{A_2}\) (đối đỉnh)
AF = AC (gt)
\(\Rightarrow\) ΔABC = ΔAFE(c.g.c) (đpcm)
18 tháng 11 2016
Bạn áp dụng trường hợp bằng nhau cạnh - góc - cạnh của tam giác rồi chứng minh nha
28 tháng 6 2021
a) Xét ΔABC có \(BC^2=AB^2+AC^2\left(5^2=3^2+4^2\right)\)
nên ΔABC vuông tại A(Định lí Pytago đảo)
b) Xét ΔABD vuông tại A và ΔEBD vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)(BD là tia phân giác của \(\widehat{ABE}\))
Do đó: ΔABD=ΔEBD(Cạnh huyền-góc nhọn)
Suy ra: DA=DE(hai cạnh tương ứng)
c) Xét ΔADF vuông tại A và ΔEDC vuông tại E có
DA=DE(cmt)
\(\widehat{ADF}=\widehat{EDC}\)(hai góc đối đỉnh)
Do đó: ΔADF=ΔEDC(Cạnh góc vuông-góc nhọn kề)
Suy ra: DF=DC(Hai cạnh tương ứng)
mà DC>DE(ΔDEC vuông tại E)
nên DF>DE
18 tháng 12 2023
Bài 3:
a: Xét tứ giác ABNC có
M là trung điểm chung của AN và BC
=>ABNC là hình bình hành
Hình bình hành ABNC có AB=AC
nên ABNC là hình thoi
b: Ta có:ABNC là hình thoi
=>AB//NC
mà D\(\in\)NC
nên AB//CD
Xét tứ giác ABCD có
AB//CD
AD//BC
Do đó: ABCD là hình bình hành
=>AD=BC
c: Xét ΔADN vuông tại A có \(DN^2=AD^2+AN^2\)
=>\(DN^2=9^2+12^2=225\)
=>\(DN=\sqrt{225}=15\left(cm\right)\)
Xét ΔAND vuông tại A có AH là đường cao
nên \(AH\cdot ND=AN\cdot AD\)
=>\(AH\cdot15=9\cdot12=108\)
=>AH=108/15=7,2(cm)
Bài 4:
a: Xét tứ giác AEMN có
AE//MN
AN//ME
Do đó: AEMN là hình bình hành
Hình bình hành AEMN có AM là phân giác của góc EAN
nên AEMN là hình thoi
b: Ta có; ΔABC cân tại A
mà AM là đường phân giác
nên AM\(\perp\)BC và M là trung điểm của BC
Xét ΔABC có
M là trung điểm của BC
MN//AB
Do đó: N là trung điểm của AC
Xét ΔABC có
M,N lần lượt là trung điểm của BC,CA
=>MN là đường trung bình của ΔABC
=>MN//AB và MN=AB/2
Ta có: MN=AB/2
MN=MD/2
Do đó: AB=MD
Xét tứ giác ABMD có
DM//AB
DM=AB
Do đó: ABMD là hình bình hành
c: Xét tứ giác AMCD có
N là trung điểm chung của AC và MD
=>AMCD là hình bình hành
Hình bình hành AMCD có \(\widehat{AMC}=90^0\)
nên AMCD là hình chữ nhật
d: Để ADCM là hình vuông thì AM=CM
=>AM=BC/2
Xét ΔABC có
AM là đường trung tuyến
\(AM=\dfrac{BC}{2}\)
Do đó: ΔABC vuông tại A
=>\(\widehat{BAC}=90^0\)
22 tháng 7 2021
1.
a. Ta có: \(AB^2+AC^2=6^2+8^2=36+64=100\)
\(BC^2=10^2=100\)
\(\Rightarrow AB^2+AC^2=BC^2\) \(\Rightarrow\Delta\)ABC vuông tại A
b. \(\Delta\)ABC vuông tại A, đường cao AH. Ta có:
AB.AC = AH.BC
hay 6.8 = AH.10
=> AH = \(\dfrac{6.8}{10}=4.8\)
LT
0
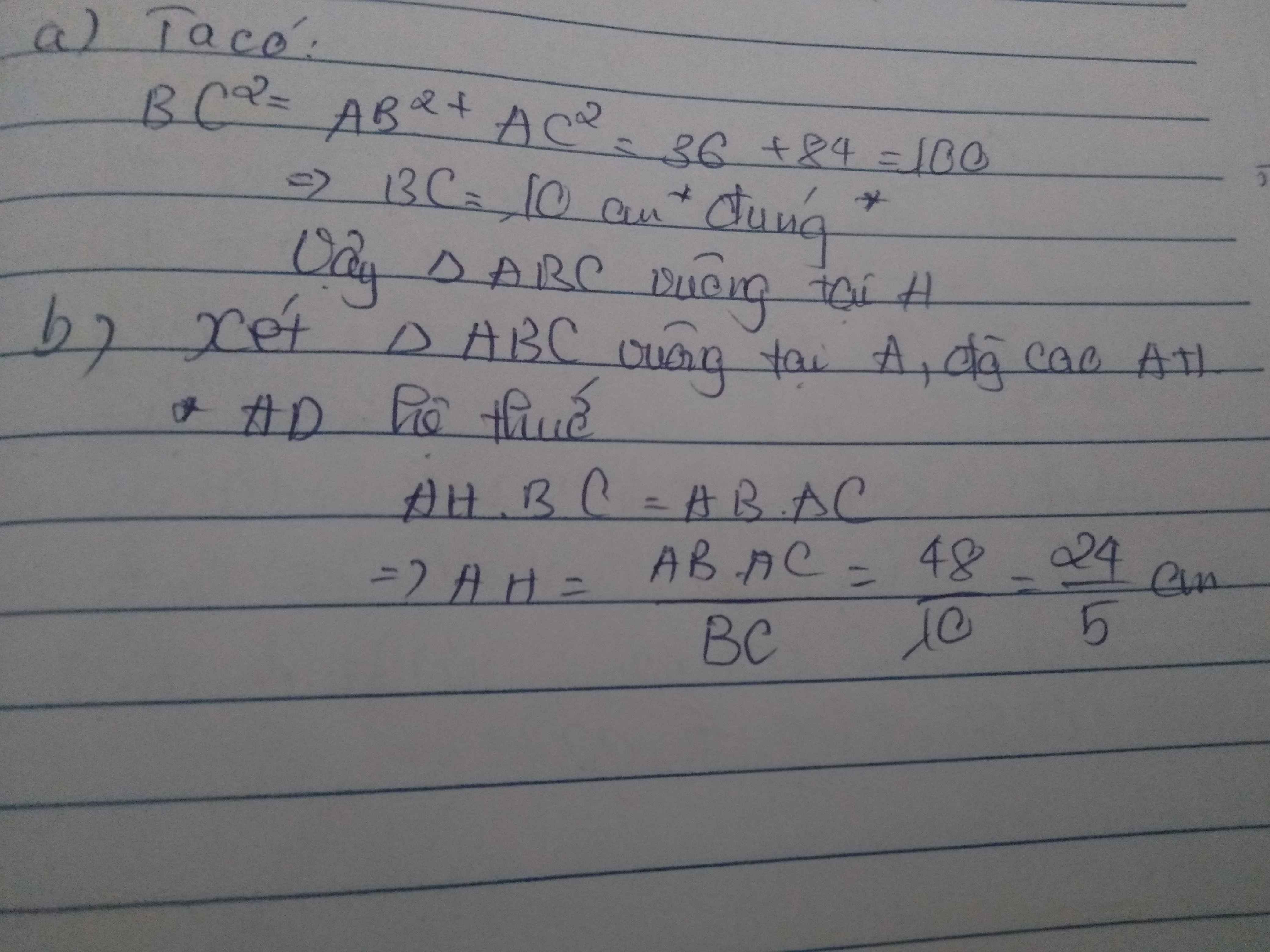
Bạn tự vẽ hình nhé :vv
Trên tia đối của tia BC lấy D sao cho AB = BD
-> B nằm giữa D và C
-> tia AB nằm giữa tia AD và tia AC
-> góc DAC > góc DAB (1)
Tam giác BAD có AB = BD (cách vẽ)
-> tam giác ABD cân tại B
-> góc DAB = góc D (2)
Từ (1)(2) -> góc DAC > góc D
Tam giác DAC có góc DAC > góc D < cmt >
-> DC > AC
Có DC = DB + BC (D nằm giữa B và C)
mà DB = AB (cmt)
-> AB + AC > BC < đpem >
Nhớ kk ạ :vv