Question

[Khánh Vy]

Trên đường thẳng xy lấy 4 điểm A ; B  ;C ; D . Từ 1 điểm O ko thuộc xy hãy vẽ các đoạn thẳng OA , OB , OC , OD 

a, Hổi trong hình vẽ có bao nhiêu tam giác đỉnh O và 2 đỉnh còn lại là 2 trong 4 điểm đã cho

b, Thay 4 điểm A,B,C,D bởi n điểm A₁; A₂;...;A_n ( n > 2 ) nằm trên đường thẳng xy . Vẽ các đoạn thẳng OA₁; OA₂ ; OA₃ , ...., OA_n . Hỏi trong hình có bao nhiêu hình tam giác đỉnh O và 2 đỉnh còn lại là 2 trong n điểm nằm trên đường thẳng xy

Answer 1

[Cua Trôi - Trường Tồn]

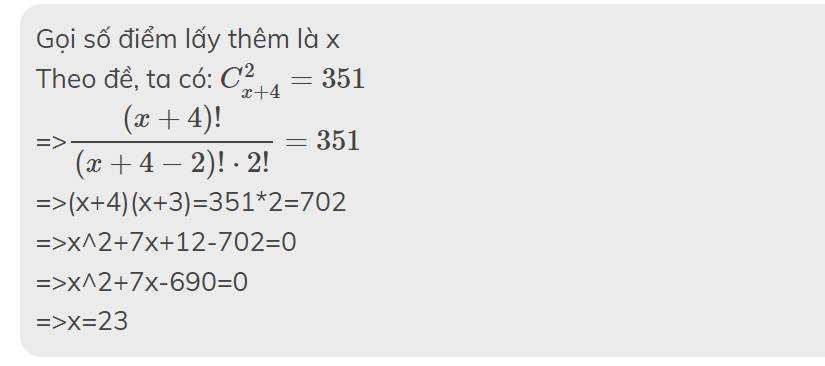
ta có hình vẽ :

a, Có 6 tam giác đỉnh O là OAB , OAC , OAD , OBC , OBD , OCD

Ta nhận thấy trên đường thẳng xy có bao nhiêu đoạn thẳng thì khi kết hợp với đỉnh O ta được bấy nhiêu tam giác

b, Nếu trên đường thẳng xy có n điểm A₁ , A₂ , ..., A_n thì số đoạn thẳng có trên đường thẳng xy là :

\(\frac{n\left(n-1\right)}{2}\)

Do đó số tam giác đỉnh O có hai đỉnh còn lại là 2 trong n điểm A₁ , A₂ ,..., A_n là \(\frac{n\left(n-1\right)}{2}\) ( tam giác ).