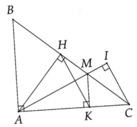
Cho tam giác ABC vuông cân tại A. Một đường thẳng a đi qua A. Gọi M và N là hình chiếu của B và C trên a
a) Chứng minh góc ABM= góc CAN
b) Chứng minh CN bằng hình chiếu của AB trên a
c) Chứng minh khi a // BC thì các hình chiếu của AB và AC trên a bằng nhau
( Vẽ hình nữa thì càng tốt nhé, mình đang cần gấp nhờ các bạn giải giúp ạ )