Cho hình bình hành ABCD có O là giao điểm hai đường chéo và thỏa AB=8cm,AD=5cm,OC=3cm.Tính độ dài của CD,BC,AC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu 28. Tổ công tác Covid-19 của bệnh viện Đại học Y Dược gồm 90 bác sĩ và 84 y tá được phân công về 1 huyện để thực hiện xét thần tốc nhằm khoanh vùng dập dịch và điều trị Covid-19 trong các khu cách ly. Muốn phục vụ được nhiều xã hơn, đội dự định chia thành các tổ sao cho số bác sĩ và y tá của các tổ bằng nhau. Hỏi có thể chia được nhiều nhất thành bao nhiêu tổ? Mỗi tổ có mấy bác sĩ, mấy y tá?
A. 12 tổ; 6 bác sĩ và 5 y tá. B. 12 tổ; 5 bác sĩ và 6 y tá.
C. 6 tổ; 15 bác sĩ và 14 y tá. D. 6 tổ; 14 bác sĩ và 15 y tá.

Theo tính chất hình bình hành ta có: I là trung điểm của AC và BD.
Suy ra:
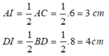
Xét tam giác AID có: A I 2 + I D 2 = A D 2 ( 3 2 + 4 2 = 5 2 = 25 )
Suy ra: tam giác AID là tam giác vuông: AI ⊥ DI hay AC ⊥ BD
Hình bình hành ABCD có 2 đường chéo AC và BD vuông góc với nhau nên là hình thoi.
Suy ra: AB = BC = CD = DA = 5cm
Chọn đáp án B

Ta có DAOK = DCOH Þ OK =OH, DDOE = DBOF Þ OE = OF Þ EHFK là hình bình hành



Ta có: ABCD là hình bình hành
\(\left\{{}\begin{matrix}CD=AB=8cm\\BC=AD=5cm\end{matrix}\right.\)
Ta có: O là giao điểm 2 đường chéo
\(\Rightarrow AC=2OC=2.3=6\left(cm\right)\)