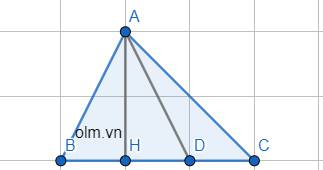
Cho tam giác nhọn A,B,C ( AB<AC ) nội tiếp đường tròn tâm (O). Vẽ đường cao AH. Gọi D,E lần lượt là hình chiếu vuông góc của H trên đường thẳng AB và AC.
a/ CM : OA\(\perp\)DE
b/ DE cắt BC tại K. CM: KH2 = KB.KC
c/ Đường thẳng KA cắt đường (O) tại F. Gọi I là tâm đường tròn ngoại tiếp tứ giác BCED. Cm F,H,I thẳng hàng.
Ai nhanh mình tik cho 3 tik nhé!