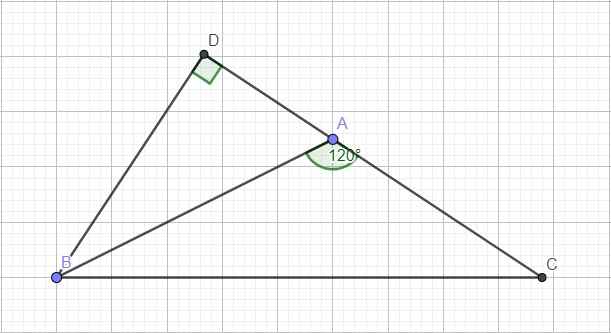
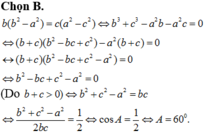Cho tam giác ABC có độ dài 3 canh là BC=a, AC=b, AB=c thoa man a2+b2>c5c2.CMR góc ABC <60 đang gấp
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
2
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 9 2021
Kẻ đường cao BD ứng với AC. Do góc A tù \(\Rightarrow\) D nằm ngoài đoạn thẳng AC hay \(CD=AD+AC\) và \(\widehat{DAB}=180^0-120^0=60^0\)
Áp dụng định lý Pitago:
\(AB^2=BD^2+AD^2\) \(\Rightarrow BD^2=AB^2-AD^2\)
Trong tam giác vuông ABD:
\(cos\widehat{BAD}=\dfrac{AD}{AB}\Rightarrow\dfrac{AD}{AB}=cos60^0=\dfrac{1}{2}\Rightarrow AD=\dfrac{1}{2}AB\)
\(\Rightarrow BD^2=AB^2-\left(\dfrac{1}{2}AB^2\right)=\dfrac{3}{4}AB^2\)
Pitago tam giác BCD:
\(BC^2=BD^2+CD^2=\dfrac{3}{4}AB^2+\left(AD+AC\right)^2\)
\(=\dfrac{3}{4}AB^2+\left(\dfrac{1}{2}AB+AC\right)^2\)
\(=\dfrac{3}{4}AB^2+\dfrac{1}{4}AB^2+AB.AC+AC^2\)
\(=AB^2+AB.AC+AC^2\)
Hay \(a^2=b^2+c^2+bc\)
P
1
18 tháng 1 2021
Gọi G là giao điểm của AM và BN.
Theo công thức tính độ dài đường trung tuyến: \(AM^2=\dfrac{2b^2+2c^2-a^2}{4}\);
\(BN^2=\dfrac{2c^2+2a^2-b^2}{4}\).
Từ đó \(AG^2=\dfrac{4}{9}AM^2=\dfrac{2b^2+2c^2-a^2}{9}\); \(BG^2=\dfrac{4}{9}BN^2=\dfrac{2c^2+2a^2-b^2}{9}\).
Do đó \(AG^2+BG^2=\dfrac{a^2+b^2+4c^2}{9}=\dfrac{9c^2}{9}=c^2=AB^2\).
Theo định lý Pythagoras đảo thì tam giác AGB vuông tại G.
Vậy góc giữa 2 trung tuyến AM và BN là 90o.
21 tháng 12 2021
bài 2:
ta có: AB<AC<BC(Vì 3cm<4cm<5cm)
=> góc C>góc A> góc B (Các cạnh và góc đồi diện trong tam giác)
Bài 3:
*Xét tam giác ABC, có:
góc A+góc B+góc c= 180 độ( tổng 3 góc 1 tam giác)
hay góc A+60 độ +40 độ=180độ
=> góc A= 180 độ-60 độ-40 độ.
=> góc A=80 độ
Ta có: góc A>góc B>góc C(vì 80 độ>60 độ>40 độ)
=> BC>AC>AB( Các cạnh và góc đối diện trong tam giác)
LN
Lưu Nguyễn Hà An
CTVHS
15 tháng 2 2022
bài 2:
ta có: AB <AC <BC (Vì 3cm <4cm <5cm)
=> góc C>góc A> góc B (Các cạnh và góc đồi diện trong tam giác)
Bài 3:
*Xét tam giác ABC, có:
góc A+góc B+góc c= 180 độ( tổng 3 góc 1 tam giác)
hay góc A+60 độ +40 độ=180độ
=> góc A= 180 độ-60 độ-40 độ.
=> góc A=80 độ
Ta có: góc A>góc B>góc C(vì 80 độ>60 độ>40 độ)
=> BC>AC>AB( Các cạnh và góc đối diện trong tam giác)
HT mik làm giống bạn Dương Mạnh Quyết
6 tháng 8 2019
Tự vẽ hình
Kẻ BH \(\perp\)AC và \(CK\perp\)AB
Tam giác AKC vuông tại K
=>CK=bsinA (1)
Tam giác BKC vuông tại K
=>CK=asinB (2)
Từ (1) (2)=>bsinA=asinB
<=>\(\frac{a}{sinA}=\frac{b}{sinB}\)
Chứng minh tương tự ta có :\(\frac{a}{sinA}=\frac{c}{sinC}\)
Vậy ....
1 tháng 4 2018
a) Trong tg ABC có góc C<A=> AB<BC( quan hệ giữa góc và cạnh đối diện trong 1 tg)
VN
30 tháng 4 2016
a. áp dụng dl Pytago ta có
BC^2= AB^2+AC^2
BC^2= 8^2+15^2=64+225=289(cm)
=> BC= căn 289=17cm
b. vì trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng 1/2 cạnh huyền nên
AM= 1/2BC= BC/2=8.5cm
AG= 2/3 AM = 2/3 . 8.5 xấp xỉ 5.7