Bạn nào giúp mình bài này với, mình làm mãi ko ra nổi. : Cho tứ diện đều ABCD ,trên các cạnh lấy 3 điểm chia đều cạnh đó. Tổng cộng có 18 điểm. Giả sử có 1 tam giác tạo thành từ 18 điểm. Tính xác xuất để tam giác đó song song duy nhất 1 cạnh của tứ diện
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
4 tháng 10 2017
Chọn D
Cách 1:
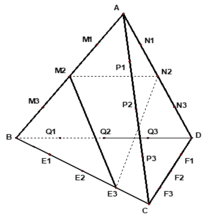
Gọi các điểm được đánh dấu để chia đều các cạnh của tứ diện đều ABCD như hình vẽ.
+ Gọi S là tập hợp các tam giác có ba đỉnh lấy từ 18 điểm đã đánh dấu.
Số phần tử của S là số cách chọn ra 3 điểm không thẳng hàng trong số 18 điểm đã cho.
Chọn ra 3 điểm trong 18 điểm trên: có C 18 3 cách.
Chọn ra 3 điểm thẳng hàng trong 18 điểm trên có 6. C 6 3 = 6 cách.
Suy ra số tam giác thỏa mãn là C 18 3 - 6 = 810
+ Gọi T là tập hợp các tam giác lấy từ ABCD sao cho mặt phẳng chứa tam giác đó song song với đúng một cạnh của tứ diện ABCD.
- Chọn 1 cạnh của tứ diện để mặt phẳng chứa tam giác chỉ song song với đúng cạnh đó: có C 6 1 cách.
Xét các tam giác mà mặt phẳng chứa nó chỉ song song với cạnh BD, suy ra tam giác đó phải có một cạnh song song với BD.
- Có 6 cách chọn cạnh song song với BD là
- Giả sử ta chọn cạnh M 2 N 2 là cạnh của tam giác. Cần chọn đỉnh thứ 3 của tam giác trong 16 điểm còn lại.
Do M 2 N 2 ⊂ (ABD) mà mặt phẳng chứa tam giác song song với BD nên đỉnh thứ 3 không thể là 7 điểm còn lại nằm trong mp(ABD).
Do mặt phẳng chứa tam giác chỉ song song với BD nên đỉnh thứ 3 không được trùng với một trong ba điểm E 2 , F 2 , P 2 . Vậy đỉnh thứ 3 chỉ được chọn trong 16 -7 - 3 = 6 điểm còn lại.
Suy ra có 6 tam giác có 1 cạnh là M 2 N 2 và mặt phẳng chứa nó chỉ song song với BD.
Vậy số tam giác mà mặt phẳng chứa nó chỉ song song với cạnh BD là: 6.6 = 36.
Tương tự cho các trường hợp khác, ta có số tam giác mà mặt phẳng chứa nó chỉ song song với đúng một cạnh của tứ diện ABCD là: 36.6 = 216.
Vậy xác suất cần tìm là
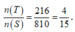
Cách 2: Lưu Thêm
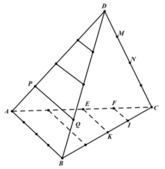
+) Gọi S là tập hợp các tam giác có ba đỉnh lấy từ 18 điểm đã đánh dấu.
Chọn ra 3 điểm trong 18 điểm trên: có C 18 3 cách.
Trong số C 18 3 đó, có 6 cách chọn ra 3 điểm thẳng hàng trên các cạnh.
Suy ra n(S) = C 18 3 - 6 = 810
+) Xét phép thử: “Lấy ngẫu nhiên một phần thử thuộc S”. Ta có 
+) Gọi T là biến cố: “Mặt phẳng chứa tam giác được chọn song song với đúng một cạnh của tứ diện đã cho”.
Chọn một cạnh của tứ diện: 6 cách, (giả sử chọn AB).
Chọn đường thẳng song song với AB: 6 cách, (giả sử chọn PQ).
Chọn đỉnh thứ 3: 6 cách, (M, N, E, K, F, I).
Suy ra n(T) = 6.6.6 = 216
Vậy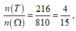 
15 tháng 5 2019
Em kham khảo link này nhé.
Câu hỏi của Trần Thị Trâm Anh - Toán lớp 5 - Học toán với OnlineMath
6 tháng 1 2019
cho địa chỉ mail mình gửi bài giải cho latuanthiendhc@gmail.com