Trên trang web của Tổng cục Thống kê có thông tin:Dân số trung bình năm 2017 của cả nước ước tính 93,7 triệu người,tăng 1,07% so với năm 2016.Hỏi nếu với mức tăng dân số như vậy thì dân số trung bình năm 2018 của cả nước ước tính là bao nhiêu người ?
Giúp mình với,mình đang cần gấp!

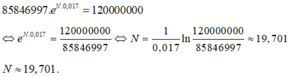



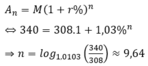
94,70259
nài này dễ mà nhi