Tìmx, y:x-1/y-2= 1/2 với x-y=3
GIÚP MÌNH NHA
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


b: \(=\dfrac{3a-9-2a-6-6}{\left(a+3\right)\left(a-3\right)}=\dfrac{a-15}{a^2-9}\)

a: Để hàm số nghịch biến trên R thì m-2<0
=>m<2
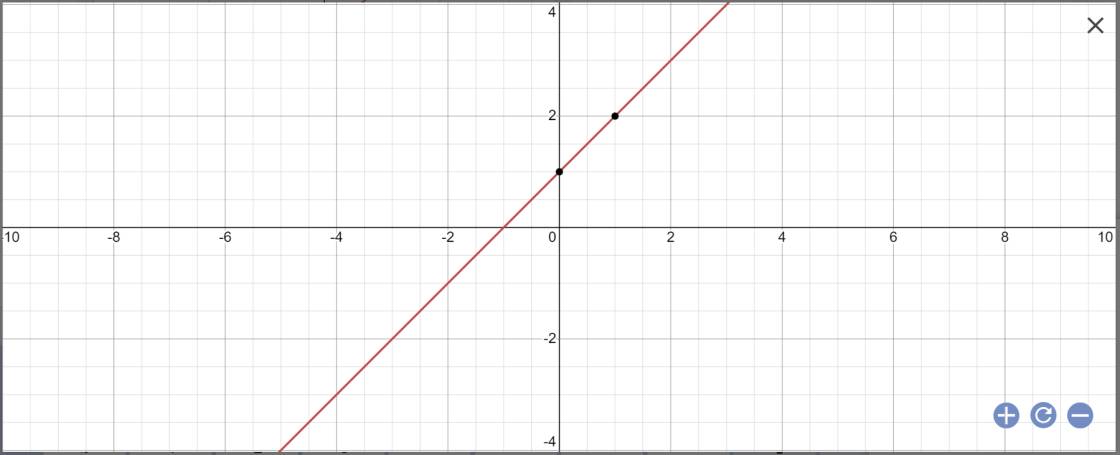
b: Khi m=3 thì y=x+1

Lời giải:
Ta có:
$A^2=(x+y)^2=x^2+y^2+2xy=2(x^2+y^2)-(x^2-2xy+y^2)$
$=2(x^2+y^2)-(x-y)^2\leq 2(x^2+y^2)$
$A^2\leq 24$
$\Rightarrow -\sqrt{24}\leq A\leq \sqrt{24}$
Vậy $A_{\max}=\sqrt{24}; A_{\min}=-\sqrt{24}$

Thay `x=-1, y=3`
`B=3*(-1)^2*3-6*(-1)^2*3^2+3*(-1)*3^2`
`= 3*3-6*9-3*9`
`= 9-54-27`
`=-72`
Câu này chắc là tính B.
\(B=3x^2y-6x^2y^2+3xy^2\\ B=3xy.\left(x-2xy+y\right)\\ Thay:x=-1;y=3.vàoB:\\ B=3.\left(-1\right).3.\left[-1-2.\left(-1\right).3+3\right]=-3.3.\left(-1+6+3\right)=-9.8=-72\)

c: Ta có: \(\left(x+1\right)^2\ge0\forall x\)
\(\left(y-\dfrac{1}{3}\right)^2\ge0\forall y\)
Do đó: \(\left(x+1\right)^2+\left(y-\dfrac{1}{3}\right)^2\ge0\forall x,y\)
\(\Leftrightarrow\left(x+1\right)^2+\left(y-\dfrac{1}{3}\right)^2-10\ge-10\forall x,y\)
Dấu '=' xảy ra khi x=-1 và \(y=\dfrac{1}{3}\)

(x + 1)(y + 2) = 5
\(\Rightarrow\) x + 1; y + 2 \(\in\) Ư(5) = {1;5}
Nếu x + 1 = 1 và y + 2 = 5 thì x = 0 và y = 3
Nếu x + 1 = 5 và y + 2 = 1 thì x = 4 và y = - 1
mà x;y \(\in\) N nên x = 0 và y = 3
Vậy x = 0 và y = 3