| GT |
Tam giác ABC AD là đường phân giác ; góc CBx = góc BAD Bx ∉ nửa mặt phẳng bờ BC có chứa điểm A |
| KL |
a) Tam giác ABE đồng dạng tam giác ADC b) BE2 = AE ✖ DE |
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KN
25 tháng 3 2020
Qua D vẽ đường thẳng song song với AC cắt AB ở K
Ta có AD là đường phân giác trong của \(\Delta ABC\)
\(\Rightarrow\frac{AC}{AB}=\frac{CD}{DB}\)(theo tính chất đường phân giác trong tam giác)
CE là đường phân giác trong của \(\Delta ABC\)nên \(\frac{AC}{BC}=\frac{EA}{EB}\)(theo tính chất đường phân giác trong tam giác)
Mà AB > BC (gt) nên \(\frac{AC}{AB}< \frac{AC}{BC}\Rightarrow\frac{DC}{DB}< \frac{EA}{EB}\)(1)
\(\Delta ABC\)có \(DK//AC\)nên \(\frac{DC}{DB}=\frac{KA}{KB}\)(2)
Từ (1) và (2) suy ra \(\frac{KA}{KB}< \frac{EA}{EB}\)
\(\Rightarrow\frac{KA}{KB}+1< \frac{EA}{EB}+1\Rightarrow\frac{AB}{KB}< \frac{AB}{EB}\Rightarrow KB>EB\)
Do đó K không trùng E. Do vậy DE cắt AC, gọi M là giao điểm của DE và AC
Ta có \(\widehat{ADE}>\widehat{DAM}\)(\(\widehat{ADE}\)là góc ngoài của \(\Delta DAM\))
Mà \(\widehat{DAM}=\widehat{DAE}\)(gt) \(\Rightarrow\widehat{ADE}>\widehat{DAE}\)
\(\Rightarrow AE>DE\)(quan hệ giữa góc và cạnh đối diện trong tam giác) (3)
Mặt khác \(\widehat{DCE}=\widehat{ECA}\left(gt\right)\)mà \(\widehat{ECA}>\widehat{CED}\)(\(\widehat{ECA}\)là góc ngoài của \(\Delta CEM\))
Do đó \(\widehat{DCE}>\widehat{CED}\Rightarrow DE>DC\)(quan hệ giữa góc và cạnh đối diện trong tam giác) (4)
Từ (3) và (4) suy ra AE > DE > DC (đpcm)
22 tháng 4 2017
Giải:
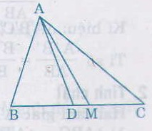
Ta có AD là đường phân giác của ∆ ABC nên
SABDSADCSABDSADC = ABACABAC = mnmn(kết quả ở bài 16)
=> SABDSADC+SABDSABDSADC+SABD= mn+mmn+m
hay SABDSABCSABDSABC= mn+mmn+m => SABMSABM= 1212 SABCSABC.
Giả sử AB < AC( m<n) vì AD là đường phân giác, AM là đường trung tuyến kẻ từ A nên AD nằm giữa AB và AM.
=> SADMSADM= SABMSABM - SABDSABD
=> SADMSADM = 1212S -mn+mmn+mS =
2 tháng 8 2018
a)
Có AB < AC (vì n > m) (1)
Ta có: \(\dfrac{AB}{AC}=\dfrac{BD}{DC}\) ( vì AD là phân giác của góc BAC) (2)
Từ (1) và (2), ta có BD < CD
⇒ D nằm giữa B và M
Đặt S1, S2 lần lượt là diện tích △ADM và △ADC
Ta có: \(\dfrac{S_1}{S_2}=\dfrac{\dfrac{1}{2}.BD.AH}{\dfrac{1}{2}.CD.AH}=\dfrac{BD}{CD}=\dfrac{AB}{AC}=\dfrac{m}{n}\)
⇒ \(\dfrac{S_1+S_2}{S_2}=\dfrac{m+n}{n}=\dfrac{S}{S_2}=\dfrac{m+n}{n}\Rightarrow S_2=\dfrac{n.S}{m+n}\)
Vì \(S_{AMC}=S_{AMB}=\dfrac{1}{2}.S\Rightarrow\)diện tích của △ADM là
\(S_{ADM}=S_{ADC}-S_{AMC}=S_2-\dfrac{1}{2}.S=\dfrac{n.S}{m+n}-\dfrac{1}{2}.S=\left[\dfrac{n-m}{2\left(m+n\right)}\right].S\)
b)
\(S_{ADM}=\left[\dfrac{7-3}{2\left(7+3\right)}\right].S=\dfrac{2}{10}.S=\dfrac{1}{5}.S=0,2.S=20\%.S\)
Vậy diện tích của △ADM bằng 20% diện tích của △ABC
17 tháng 9 2023
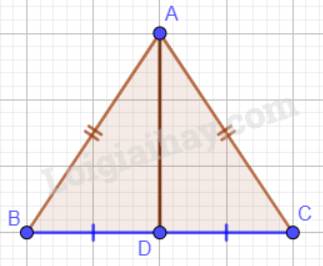
AD là phân giác của góc A nên \(\widehat {BAD} = \widehat {CAD}\).
Xét tam giác ABD và tam giác ACD có:
AB = AC (tam giác ABC cân tại A);
\(\widehat {BAD} = \widehat {CAD}\);
AD chung
Vậy \(\Delta ABD = \Delta ACD\)(c.g.c) nên \(BD = CD\) (2 cạnh tương ứng)
\(\Rightarrow\) D là trung điểm của cạnh BC.
Vì \(\Delta ABD = \Delta ACD\) nên \(\widehat {ADB} = \widehat {ADC}\) ( 2 góc tương ứng).
Mà \(\widehat {ADB} + \widehat {ADC}=180^0\) (2 góc kề bù) nên \(\widehat {ADB} = \widehat {ADC} = 90^\circ \Rightarrow AD \bot BC\).
Vậy AD là đường trung trực của tam giác ABC.