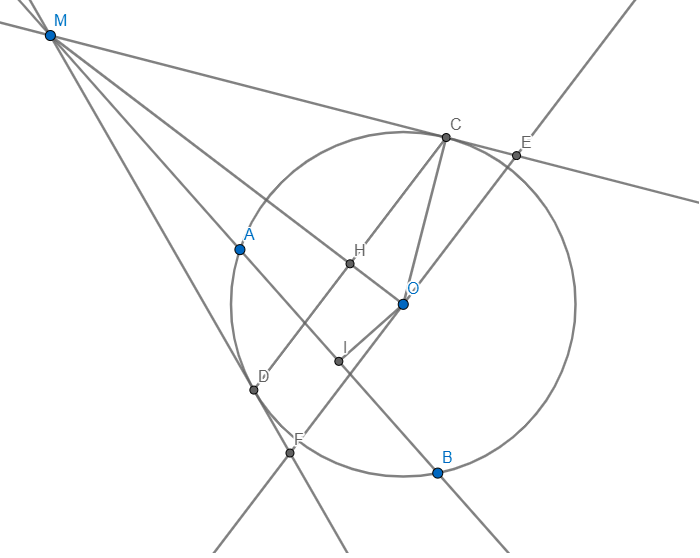
Cho đường tròn(O)bán kính r và đường thẳng (d) không đi qua O, cắt đường tròn (O) tại 2 điểm E,F. Lấy điểm M bất kì trên tia đối FE, qua M kẻ 2 tiếp tuyến MC,MD với đường tròn(C,D là các tiếp điểm)
1) Chứng minh tứ giácMCOD nội tiếp trong 1 nửa đường tròn
2) gọi K là trung điểm của đoạn thẳng EF. Chứng minh KM là phâm giác của góc CKD.
3) đường thẳng đi qua O và vuông góc với MO cắt các tia MC, MD thao thứ tự tại R, T. Tìm vị trí của điểm M trên (d) sao cho diền tích tam giác MRT nhỏ nhất.