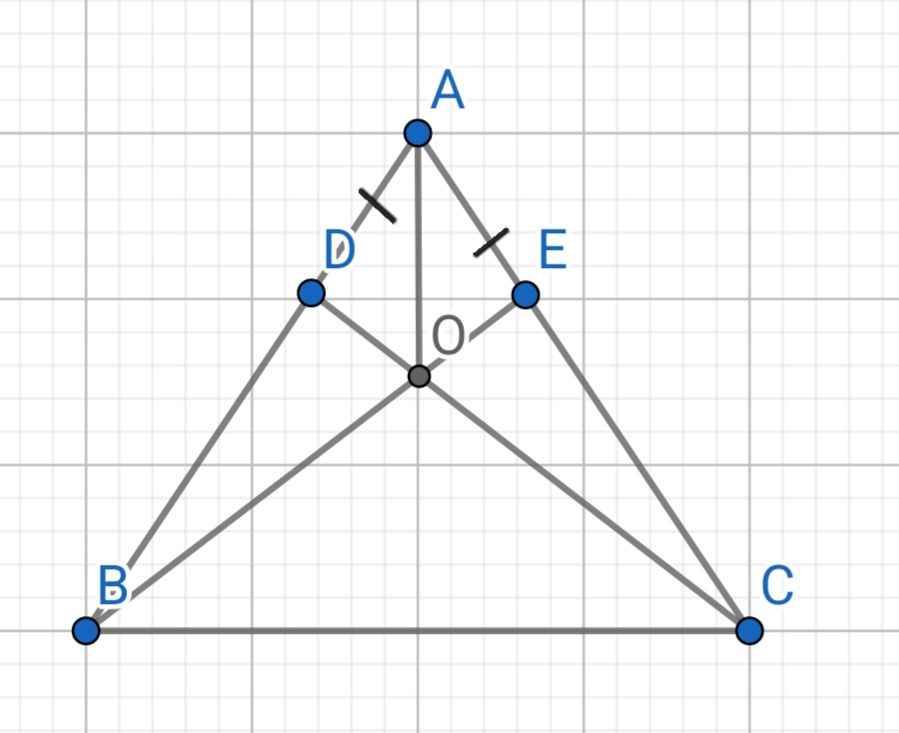
cho tam giác abc cân tại a trên cạnh ab lấy điểm d trên cạnh ac lấy điểm e sao cho ad = ae.Gọi I là giao điểm của BE và Cd .CMR
a)DE//BC
b) AI là tia phân giac goác bac
d) AI vuông góc vs BC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
10 tháng 4 2023
a: Xet ΔAEB và ΔADC có
AE=AD
góc A chung
AB=AC
=>ΔAEB=ΔADC
=>BE=CD
b: Xet ΔKDB và ΔKEC có
góc KDB=góc KEC
DB=EC
góc KBD=góc KCE
=>ΔKBD=ΔKCE
c: Xét ΔABK và ΔACK có
AB=AC
BK=CK
AK chung
=>ΔABK=ΔACK
=>góc BAK=góc CAK
=>AK là phân giác của góc BAC
d: ΔABC cân tại A
mà AI là phân giác
nên AI vuông góc BC
14 tháng 6 2023
a: Xét ΔABC có AD/AB=AE/AC
nên DE//BC
b: Xét ΔABE và ΔACD có
AB=AC
góc A chung
AE=AD
=>ΔABE=ΔACD
c: Xét ΔIDB và ΔIEC có
góc IDB=góc IEC
DB=EC
góc IBD=góc ICE
=>ΔIDB=ΔIEC
d: Xét ΔABI và ΔACI có
AB=AC
BI=CI
AI chung
=>ΔABI=ΔACI
=>góc BAI=góc CAI
=>AI là phân giác của góc BAC
2 tháng 4 2023
a: Xét ΔACB có AD/AB=AE/AC
nên DE//BC
b: Xet ΔABE và ΔACD có
AB=AC
góc A chung
AE=AD
=>ΔABE=ΔACD
c: Xét ΔIDB và ΔIEC có
góc IDB=góc IEC
DB=EC
góc IBD=góc ICE
=>ΔIDB=ΔIEC
d: Xét ΔAIB và ΔAIC có
AI chung
IB=IC
AB=AC
=>ΔAIB=ΔAIC
=>góc BAI=góc CAI
=>AI là phan giác của góc BAC
e: ΔBCA cân tại A
mà AI là phângíac
nên AI vuông góc BC
KV
13 tháng 11 2023
∆ABC có:
AB = AC (gt)
⇒ ∆ABC cân tại A
⇒ ∠ABC = ∠ACB
⇒ ∠DBC = ∠ECB
Do AB = AC (gt)
AD = AE (gt)
⇒ BD = AB - AD = AC - AE = CE
Xét ∆DBC và ∆ECB có:
DB = EC (cmt)
∠DBC = ∠ECB (cmt)
BC là cạnh chung
⇒ ∆DBC = ∆ECB (c-g-c)
⇒ ∠BDC = ∠CEB (hai góc tương ứng)
⇒ ∠BDO = ∠CEO
Do ∆DBC = ∆ECB (cmt)
⇒ ∠BCD = ∠CBE (hai góc tương ứng)
Mà ∠ACB = ∠ABC (cmt)
⇒ ∠ECO = ∠ACB - ∠BCD
= ∠ABC - ∠CBE
= ∠DBO
Xét ∆BOD và ∆COE có:
∠DBO = ∠ECO (cmt)
BD = CE (cmt)
∠BDO = ∠CEO (cmt)
⇒ ∆BOD = ∆COE (g-c-g)
⇒ OD = OE (hai cạnh tương ứng)
Xét ∆ADO và ∆AEO có:
AD = AE (gt)
AO là cạnh chung
OD = OE (cmt)
∆ADO = ∆AEO (c-c-c)
⇒ ∠DAO = ∠EAO (hai góc tương ứng)
⇒ AO là tia phân giác của ∠DAE
Hay AO là tia phân giác của ∠BAC
14 tháng 8 2023
a: Xét ΔADC và ΔAEB có
AD=AE
góc DAC chung
AC=AB
=>ΔADC=ΔAEB
b: AD+DB=AB
AE+EC=AC
mà AB=AC và AD=AE
nên DB=EC
Xét ΔDBC và ΔECB có
DB=EC
góc DBC=góc ECB
BC chung
=>ΔDBC=ΔECB
=>góc KBC=góc KCB
=>ΔKBC cân tại K