Tính giá trị biểu thức:
\(R=\dfrac{2}{\sqrt{4-3\sqrt[4]{5}+2\sqrt{5}-\sqrt[4]{125}}}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
RK
30 tháng 6 2021
T = \(\dfrac{\sqrt{5}\left(\sqrt{16}-\sqrt{9}\right)}{4-5}-5\sqrt{5}+\dfrac{1}{\sqrt{5}-2}+2\sqrt{5}\)
= \(-\sqrt{5}-5\sqrt{5}+2\sqrt{5}+\dfrac{1}{\sqrt{5}-2}\)
= \(-4\sqrt{5}+\dfrac{1}{\sqrt{5}-2}\)
= \(\dfrac{-4\sqrt{5}\left(\sqrt{5}-2\right)+1}{\sqrt{5}-2}\)
= \(\dfrac{-20+8\sqrt{5}+1}{\sqrt{5}-2}\)
= \(\dfrac{-19+8\sqrt{5}}{\sqrt{5}-2}\)
= \(\dfrac{19-8\sqrt{5}}{2-\sqrt{5}}\)
= \(\dfrac{\left(-2+3\sqrt{5}\right)\left(\sqrt{5}-2\right)}{-\left(\sqrt{5}-2\right)}=2-3\sqrt{5}\)
PM
1
9 tháng 11 2014
Đặt \(\sqrt[4]{5}=x\) thì \(x^4=5\). Ta có :
A = \(\frac{2}{\sqrt{4-3x+2x^2-x^3}}\)= \(\frac{2\left(x+1\right)}{\sqrt{\left(x+1\right)^2\left(4-3x+2x^2-x^3\right)}}\)= \(\frac{2\left(x+1\right)}{\sqrt{-x^5+5x+4}}\)
Ta thấy \(-x^5+5x\) = \(x\left(5-x^4\right)\)= \(0\)
nên A = \(\frac{2\left(x+1\right)}{\sqrt{4}}\)= \(x+1\)=\(\sqrt[4]{5}+1\)
12 tháng 9 2021
Bài 2:
\(x=\sqrt{4+2\sqrt{3}}=\sqrt{3}+1\)
Ta có: \(P=x^2-2x+2020\)
\(=4+2\sqrt{3}-2\left(\sqrt{3}-1\right)+2020\)
\(=4+2\sqrt{3}-2\sqrt{3}+2+2020\)
=2026
12 tháng 9 2021
Bài 1:
\(A=-\dfrac{3}{4}\cdot\sqrt{9-4\sqrt{5}}\cdot\sqrt{\left(-8\right)^2\cdot\left(2+\sqrt{5}\right)^2}\)
\(=\dfrac{-3}{4}\cdot8\cdot\left(\sqrt{5}-2\right)\left(\sqrt{5}+2\right)\)
=-6
H9
HT.Phong (9A5)
CTVHS
1 tháng 9 2023
a) \(\sqrt{3+2\sqrt{2}}+\sqrt{\left(\sqrt{2}-2\right)^2}\)
\(=\sqrt{\left(\sqrt{2}\right)^2+2\sqrt{2}\cdot1+1^2}+\left|\sqrt{2}-2\right|\)
\(=\sqrt{\left(\sqrt{2}+1\right)^2}-\left(\sqrt{2}-2\right)\)
\(=\left|\sqrt{2}+1\right|-\sqrt{2}+2\)
\(=\sqrt{2}+1-\sqrt{2}+2\)
\(=3\)
b) \(\dfrac{1}{5}\sqrt{50}-2\sqrt{96}-\dfrac{\sqrt{30}}{\sqrt{15}}+12\sqrt{\dfrac{1}{6}}\)
\(=\dfrac{1}{5}\cdot5\sqrt{2}-2\cdot4\sqrt{6}-\sqrt{\dfrac{30}{15}}+\sqrt{\dfrac{144}{6}}\)
\(=\sqrt{2}-8\sqrt{6}-\sqrt{2}+2\sqrt{6}\)
\(=-8\sqrt{6}+2\sqrt{6}\)
\(=-6\sqrt{6}\)
c) \(\left(\dfrac{5-\sqrt{5}}{\sqrt{5}}-2\right)\left(\dfrac{4}{1+\sqrt{5}}+4\right)\)
\(=\left[\dfrac{\sqrt{5}\left(\sqrt{5}-1\right)}{\sqrt{5}}-2\right]\left[\dfrac{4\left(1-\sqrt{5}\right)}{\left(1+\sqrt{5}\right)\left(1-\sqrt{5}\right)}+4\right]\)
\(=\left(\sqrt{5}-1-2\right)\left(\dfrac{4\left(1-\sqrt{5}\right)}{1-5}+4\right)\)
\(=\left(\sqrt{5}-3\right)\left(\sqrt{5}-1+4\right)\)
\(=\left(\sqrt{5}-3\right)\left(\sqrt{5}+3\right)\)
\(=\left(\sqrt{5}\right)^2-3^2\)
\(=-4\)
1 tháng 9 2023
a) \(\sqrt[]{3+2\sqrt[]{2}}+\sqrt[]{\left(\sqrt[]{2}-2\right)^2}\)
\(=\sqrt[]{2+2\sqrt[]{2}.1+1}+\left|\sqrt[]{2}-2\right|\)
\(=\sqrt[]{\left(\sqrt[]{2}+1\right)^2}+\left(2-\sqrt[]{2}\right)\) \(\left(\left(\sqrt[]{2}\right)^2=2< 2^2=4\right)\)
\(=\left|\sqrt[]{2}+1\right|+2-\sqrt[]{2}\)
\(=\sqrt[]{2}+1+2-\sqrt[]{2}\)
\(=3\)
I
1
NV
Nguyễn Việt Lâm
Giáo viên
15 tháng 9 2021
Bài này nằm trong cuốn nâng cao và phát triển của Vũ Hữu Bình, và lời giải của nó thực sự rất "ảo". Có lẽ trừ tác giả ra, khó ai mà nghĩ được ra cách giải:
AH
Akai Haruma
Giáo viên
1 tháng 4 2021
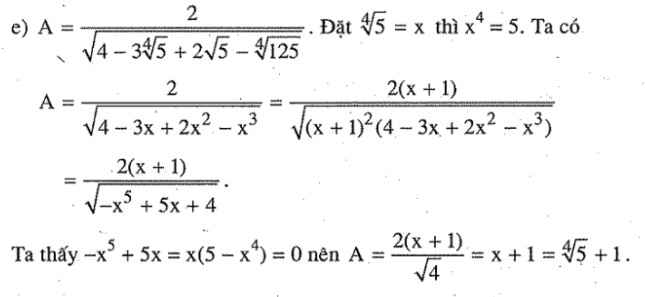
Lời giải:
ĐKXĐ: $x\geq 0; x\neq 1; x\neq 25$
a)
\(A=\frac{4\sqrt{x}}{\sqrt{x}-5}:\left[\frac{(\sqrt{x}-2)(\sqrt{x}+2)+\sqrt{x}-1}{(\sqrt{x}-1)(\sqrt{x}+2}+\frac{5-2\sqrt{x}}{(\sqrt{x}-1)(\sqrt{x}+2)}\right]\)
\(=\frac{4\sqrt{x}}{\sqrt{x}-5}:\frac{x-4+\sqrt{x}-1+5-2\sqrt{x}}{(\sqrt{x}-1)(\sqrt{x}+2)}\)
\(=\frac{4\sqrt{x}}{\sqrt{x}-5}:\frac{\sqrt{x}(\sqrt{x}-1)}{(\sqrt{x}-1)(\sqrt{x}+2)}=\frac{4\sqrt{x}}{\sqrt{x}-5}:\frac{\sqrt{x}}{\sqrt{x}+2}=\frac{4\sqrt{x}}{\sqrt{x}-5}.\frac{\sqrt{x}+2}{\sqrt{x}}=\frac{4(\sqrt{x}+2)}{\sqrt{x}-5}\)
b) Tại $x=81$ thì $\sqrt{x}=9$.
Khi đó: $A=\frac{4(9+2)}{9-5}=11$
c) $A< 4\Leftrightarrow \frac{\sqrt{x}+2}{\sqrt{x}-5}< 1$
$\Leftrightarrow \frac{7}{\sqrt{x}-5}< 0\Leftrightarrow \sqrt{x}-5< 0$
$\Leftrightarrow 0\leq x< 25$. Kết hợp với ĐKXĐ suy ra: $0\leq x< 25; x\neq 1$
D
2
11 tháng 5 2022
\(A=\left(3\cdot\dfrac{\sqrt{2}-1}{2}-5\right):\left(2\cdot\dfrac{\sqrt{2}-1}{2}+1\right)\)
\(=\dfrac{3\sqrt{2}-3-10}{2}\cdot\dfrac{1}{\sqrt{2}}=\dfrac{6-13\sqrt{2}}{4}\)
H
11 tháng 5 2022
\(x=\dfrac{3-2\sqrt{2}}{4}=\dfrac{2-2\sqrt{2}+1}{4}=\dfrac{\left(\sqrt{2}-1\right)^2}{4}=\left(\dfrac{\sqrt{2}-1}{2}\right)^2\)
\(A=\dfrac{3\sqrt{\left(\dfrac{\sqrt{2}-1}{2}\right)^2}-5}{2\sqrt{\left(\dfrac{\sqrt{2}-1}{2}\right)^2}+1}=\dfrac{\dfrac{3\sqrt{2}-3}{2}-5}{\sqrt{2}-1+1}=\dfrac{3\sqrt{2}-3-10}{2}.\dfrac{1}{\sqrt{2}}=\dfrac{3\sqrt{2}-13}{2\sqrt{2}}=\dfrac{6-13\sqrt{2}}{4}\)
\(R=\dfrac{2}{\sqrt{3-\sqrt{5}-\left(\sqrt[4]{5}-1\right)^3}}=\dfrac{2}{\sqrt{\dfrac{\left(\sqrt{5}-1\right)^2}{2}-\left(\sqrt[4]{5}-1\right)^3}}\)
\(=\dfrac{2}{\sqrt{\dfrac{\left(\sqrt[4]{5}-1\right)^2\left(\sqrt[4]{5}+1\right)^2}{2}-\left(\sqrt[4]{5}-1\right)^3}}\)
\(=\dfrac{2\sqrt{2}}{\sqrt{\left(\sqrt[4]{5}-1\right)^2\left[\left(\sqrt[4]{5}+1\right)^2-2\left(\sqrt[4]{5}-1\right)\right]}}\)
\(=\dfrac{2\sqrt{2}}{\left(\sqrt[4]{5}-1\right)\sqrt{\sqrt{5}+2\sqrt[4]{5}+1-2\sqrt[4]{5}+2}}\)
\(=\dfrac{2\sqrt{2}}{\left(\sqrt[4]{5}-1\right)\sqrt{3+\sqrt{5}}}=\dfrac{2\sqrt{2}}{\left(\sqrt[4]{5}-1\right)\sqrt{\dfrac{\left(\sqrt{5}+1\right)^2}{2}}}\)
\(=\dfrac{4}{\left(\sqrt[4]{5}-1\right)\left(\sqrt{5}+1\right)}=\dfrac{4\left(\sqrt[4]{5}+1\right)}{\left(\sqrt[4]{5}+1\right)\left(\sqrt[4]{5}-1\right)\left(\sqrt{5}+1\right)}\)
\(\)\(=\dfrac{4\left(\sqrt[4]{5}+1\right)}{\left(\sqrt{5}-1\right)\left(\sqrt{5}+1\right)}=\dfrac{4\left(\sqrt[4]{5}+1\right)}{4}\)
\(=\sqrt[4]{5}+1\)
R = \(\sqrt[4]{5}+1\)