Viết thuật toán liệt kê hoặc sơ đồ khối:
Tính \(S=\dfrac{1}{2}+\dfrac{3}{4}+\dfrac{5}{6}+...+\dfrac{2n+1}{2n+2}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
22 tháng 2 2022
a: \(M=\dfrac{6}{5}+\dfrac{3}{2}\left(\dfrac{2}{5\cdot7}+...+\dfrac{2}{97\cdot99}+\dfrac{2}{99\cdot101}\right)\)
\(=\dfrac{6}{5}+\dfrac{3}{2}\left(\dfrac{1}{5}-\dfrac{1}{101}\right)\)
\(=\dfrac{6}{5}+\dfrac{3}{10}-\dfrac{3}{202}=\dfrac{150}{101}\)
b: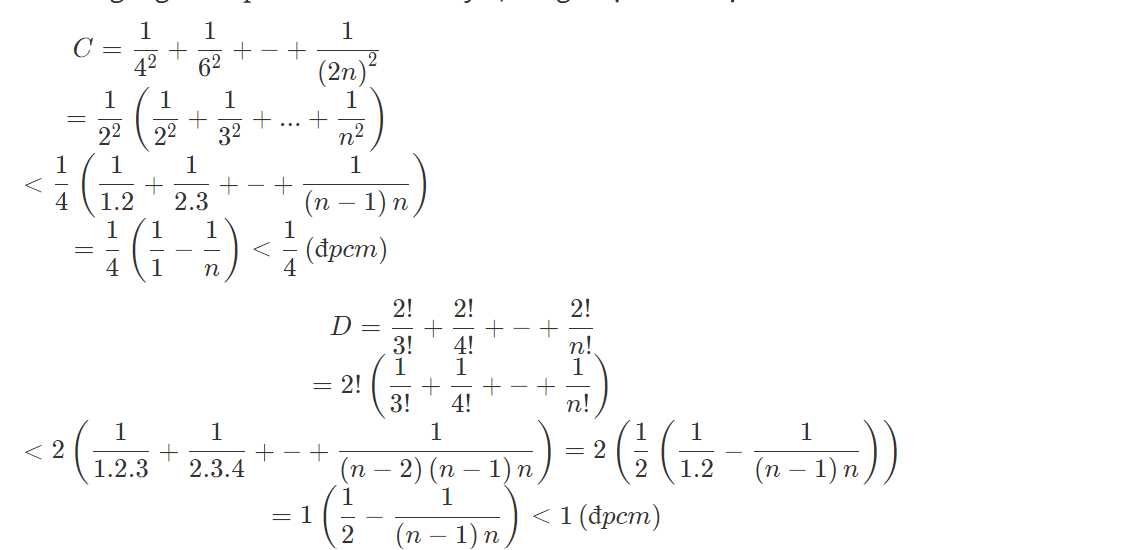 
22 tháng 11 2018
a) Đặt \(A=\dfrac{1}{2^2}+\dfrac{1}{4^2}+\dfrac{1}{6^2}+...+\dfrac{1}{\left(2n\right)^2}\)
\(A=\dfrac{1}{2^2}\left(1+\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{n^2}\right)\)
Ta có:
\(\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{n^2}< \dfrac{1}{1.2}+\dfrac{1}{2.3}+...+\dfrac{1}{\left(n-1\right)n}\)
\(\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{n^2}< 1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{n-1}-\dfrac{1}{n}\)
\(\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{n^2}< 1-\dfrac{1}{n}\)
\(\Rightarrow1+\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{n^2}< 1-\dfrac{1}{n}+1\)
\(\Rightarrow1+\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{n^2}< 2-\dfrac{1}{n}\)
\(\Rightarrow\dfrac{1}{2^2}\left(1+\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{n^2}\right)< \dfrac{1}{2^2}\left(2-\dfrac{1}{2}\right)\)
\(\Rightarrow A< \dfrac{1}{2^2}.2-\dfrac{1}{2^2}.\dfrac{1}{2}\)
\(\Rightarrow A< \dfrac{1}{2}-\dfrac{1}{2^3}< \dfrac{1}{2}\)
Vậy \(A< \dfrac{1}{2}\left(Đpcm\right)\)
b) Đặt \(B=\dfrac{1}{3^2}+\dfrac{1}{5^2}+\dfrac{1}{7^2}+...+\dfrac{1}{\left(2n+1\right)^2}\)
Ta có:
\(B< \dfrac{1}{1.3}+\dfrac{1}{3.5}+\dfrac{1}{5.7}+...+\dfrac{1}{\left(2n-1\right)\left(2n+1\right)}\)
\(B< \dfrac{1}{2}\left(\dfrac{2}{1.3}+\dfrac{2}{3.5}+\dfrac{2}{5.7}+...+\dfrac{2}{\left(2n-1\right)\left(2n+1\right)}\right)\)
\(B< \dfrac{1}{2}\left(1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{1}{2n-1}-\dfrac{1}{2n+1}\right)\)
\(B< \dfrac{1}{2}\left(1-\dfrac{1}{2n+1}\right)\)
\(B< \dfrac{1}{2}\left(\dfrac{2n+1}{2n+1}-\dfrac{1}{2n+1}\right)\)
\(B< \dfrac{1}{2}.\dfrac{2n}{2n+1}\)
\(B< \dfrac{2n}{4n+2}\)
\(B< \dfrac{2n}{2\left(2n+1\right)}\)
\(B< \dfrac{n}{2n+1}\)
30 tháng 12 2020
Bài 1:
Ý tưởng: Sau khi nhập bán kính r, chúng ta sẽ tính diện tích theo công thức \(S=r^2\cdot pi\)
Xác định bài toán
-Input: Bán kính r
-Output: Diện tích hình tròn có bán kính r
Mô tả thuật toán
-Bước 1: Nhập r
-Bước 2: \(s\leftarrow pi\cdot sqr\left(r\right)\)
-Bước 3: Xuất s
-Bước 4: Kết thúc
Bài 2:
Ý tưởng: Sau khi nhập cạnh a chúng ta sẽ tính chu vi hình vuông có cạnh a theo công thức \(S=4\cdot a\)
Xác định bài toán:
-Input: Cạnh a
-Output: Chu vi hình vuông có cạnh a
Mô tả thuật toán
-Bước 1: Nhập a
-Bước 2: s←a*4;
-Bước 3: Xuất s
-Bước 4: Kết thúc
5 tháng 1 2018
program Bai_1;
uses crt;
var n,i:integer; s:real;
begin
clrscr;
write('Nhap n: '); readln(n);
for i:=1 to n do s:=s+1/(2*i);
write('S=',s);
readln;
end.
program Bai_2;
uses crt;
var n,i:integer; gt:longint; s:real;
begin
clrscr;
write('n='); readln(n);
gt:=1;
for i:=1 to n do
begin
gt:=gt*i;
s:=s+1/gt;
end;
write('S=',s);
readln;
end.
7 tháng 1 2018
- nếu như khai báo biến S:real thì nên thêm độ rộng chữ số vào kq
13 tháng 12 2017
Program bai1;
uses crt;
var n,i: integer;
s:real;
begin
clrscr;
s:=0;
write('nhap n ='); readln(n);
for i:= 1 to n do
s:=s+(2*i-1)/(2*i);
writeln('S = ' ,s :4:2);
readln;
end.
TV
1
7 tháng 1 2022
#include <bits/stdc++.h>
using namespace std;
int t,i;
int main()
{
t=0;
for (i=1; i<=10; i++) t=t+i;
cout<<t;
return 0;
}