Trong một bình nước rộng có một lớp dầu dày d = 1,0cm. Người ta thả vào bình một cốc hình trụ thành mỏng, có khối lượng m = 4,0g và có diện tích đáy S = 25cm2. Lúc đầu cốc không chứa gì, đáy cốc nằm cao hơn điểm chính giữa của lớp dầu. Sau đó rót dầu vào cốc tới miệng thì mực dầu trong cốc cũng ngang mực dầu trong bình. Trong cả hai trường hợp đáy cốc đều cách mặt nước cùng một khoảng bằng a (hình vẽ 2). Xác định khối lượng riêng ρ1 của dầu, biết khối lượng riêng của nước là ρ0 = 1,0g/cm3.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan

CM
5 tháng 2 2019
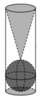
Gọi bán kính đáy của cốc hình trụ là R. Suy ra chiều cao của cốc nước hình trụ là 6R bán kính của viên bi là R; bán kính đáy hình nón là R; chiều cao của hình nón là 4R
Thể tích khối nón là ![]() Thể tích khối nón là
Thể tích khối nón là ![]()
Thể tích của cốc (thể tích lượng nước ban đầu) là ![]()
Suy ra thể tích nước còn lại: ![]() Vậy
Vậy 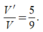
Chọn D.









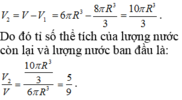
Lúc đầu cốc không chứa gì và nổi trong dầu thì trọng lượng của cốc cân bằng với lực đẩy Acsimet của dầu:
10.mcốc = FA1 = 10(d - a)S.ρ1 (1)
Sau khi rót dầu tới miệng cốc rồi thả vào bình thì trọng lượng của cốc dầu cân bằng lực đẩy Acsimet của nước và dầu:
10.mcốc + 10(d + a)S.ρ1 = FA2 = 10.d.S.ρ1 + 10.a.S.ρ0 (2)
Thay (1) vào (2) rồi rút gọn ta được:d.ρ1 = a.ρ0
\(\Rightarrow a=d\dfrac{\text{ρ}_1}{\text{ρ}_0}\left(3\right)\)
thay 3 vaof 1 giai pt
p1 p0 là gì vậy bn