Cho hình thang IKLM. Biết rằng NI = NM và PK = PL. Độ dài đoạn IK = 24cm, ML = 24cm.
Độ dài NP
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
2 tháng 3 2022
a: Xét ΔMNP có \(MP^2=NM^2+NP^2\)
nên ΔMNP vuông tại N
b: \(PK=\sqrt{8^2+6^2}=10\left(cm\right)\)
NT
0
2 tháng 3 2022
a: Xét ΔMNP có \(MP^2=NP^2+NM^2\)
nên ΔMNP vuông tại N
b: \(PK=\sqrt{6^2+8^2}=10\left(cm\right)\)
9 tháng 4 2022
Cho đoạn thẳng PQ có độ dài bằng 7cm. Trên tia PQ, lấy điểm K và L sao cho Pk = 2cm, PL = 4cm. Độ dài đoạn thẳng KL là
A. 1cm B. 3cm C. 2cm D. 5cm
12 tháng 11 2023
Bài 1:
ΔDMK vuông tại M
=>\(DM^2+MK^2=DK^2\)
=>\(DM^2=12^2-10^2=44\)
=>\(DM=2\sqrt{11}\left(cm\right)\)
ΔDMN vuông tại D
=>\(DM^2+DN^2=MN^2\)
=>\(DN^2+44=324\)
=>\(DN^2=280\)
=>\(DN=2\sqrt{70}\left(cm\right)\)
Bài 2:
ΔGNH vuông tại G
=>\(GN^2+GH^2=HN^2\)
=>\(HN^2=8^2+12^2=208\)
=>\(HN=4\sqrt{13}\left(cm\right)\)
Xét ΔGNH vuông tại G có \(cosGNH=\dfrac{GN}{HN}=\dfrac{2}{\sqrt{13}}\)
=>\(cosNHM=\dfrac{2}{\sqrt{13}}\left(\widehat{GNH}=\widehat{NHM}\right)\) do GN//HM
Xét ΔNHM có \(cosNHM=\dfrac{HN^2+HM^2-NM^2}{2\cdot HN\cdot HM}\)
=>\(\dfrac{52+HM^2-484}{2\cdot4\sqrt{13}\cdot HM}=\dfrac{2}{\sqrt{13}}\)
=>\(HM^2-432=\dfrac{2}{\sqrt{13}}\cdot2\cdot4\sqrt{13}\cdot HM\)
=>\(HM^2-432=16HM\)
=>\(HM^2-16HM-432=0\)
=>\(\left[{}\begin{matrix}HM=8+4\sqrt{31}\left(cm\right)\left(nhận\right)\\HM=8-4\sqrt{31}\left(loại\right)\end{matrix}\right.\)
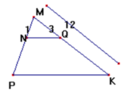
Xét hình thang IKLM có
N là trung điểm của IM
P là trung điểm của KL
Do đó: NP là đường trung bình của hình thang IKLM
\(\Leftrightarrow NP=\dfrac{IK+ML}{2}=\dfrac{24+24}{2}=24\left(cm\right)\)