Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a:
ΔABC vuông tại A có AB=AC
nên ΔABC vuông cân tại A
=>góc ABC=góc ACB=45 độ
góc BDA=1/2*sđ cung BA=90 độ
góc EAC=1/2*sđ cung CA=90 độ
BD vuông góc DA
CE vuông góc AE
mà D,A,E thẳng hàng
nên BD//CE
Xét tứ giác BDEC có
góc BDE+góc DEC+góc DBC+góc ECB=360 độ
=>góc DBC+góc ECB=180 độ
=>góc ECA+góc ACB+góc ABD+góc ABC=180 độ
=>góc ECA+góc ABD=90 độ
góc EAC+góc ECA=90 độ
mà góc DBA+góc ECA=90 độ
nên góc EAC=góc DBA
Xét ΔACE vuông tại E và ΔBAD vuông tại D có
AC=AB
góc EAC=góc DBA
=>ΔACE=ΔBAD
=>AD=CE
b: AD^2+AE^2
=CE^2+AE^2
=AC^2=16
a: góc HIB=1/2*sđ cung HB=90 độ
=>HI vuông góc AB
góc CKH=1/2*sđ cung CH=90 độ
=>HK vuông góc AC
góc AIH=góc AKH=góc KAI=90 độ
=>AIHK là hình chữ nhật
=>góc AIK=góc AHK=góc C
=>góc KIB+góc KCB=180 độ
=>KIBC nội tiếp
b: góc O1IK=góc O1IH+góc KIH
=góc O1HI+góc KAH
=góc HAC+góc HCA=90 độ
=>IK làtiếp tuyến của (O1)
góc O2KI=góc O2KH+góc IKH
=góc O2HK+góc IAH
=góc HAB+góc HBA=90 độ
=>IK là tiếp tuyến của (O2)
Xét đường tròn đường kính HB có
ΔHMB nội tiếp đường tròn
HB là đường kính
Do đó: ΔHMB vuông tại M
Xét đường tròn đường kính HC có
ΔHNC nội tiếp đường tròn
HC là đường kính
Do đó: ΔHNC vuông tại N
Xét tứ giác AMHN có
\(\widehat{NAM}=\widehat{ANH}=\widehat{AMH}=90^0\)
nên AMHN là hình chữ nhật
Xét đường tròn đường kính HB có
ΔHMB nội tiếp đường tròn
HB là đường kính
Do đó: ΔHMB vuông tại M
Xét đường tròn đường kính HC có
ΔHNC nội tiếp đường tròn
HC là đường kính
Do đó: ΔHNC vuông tại N
Xét tứ giác AMHN có
\(\widehat{NAM}=\widehat{ANH}=\widehat{AMH}=90^0\)
nên AMHN là hình chữ nhật
Bạn muốn nhận giày và balo miễn phí cho năm học mới? --->Tham gia ngay Minigame NHANH NHƯ CHỚP số thứ 7 ngày 16/02/2019 tại đây: https://alfazi.edu.vn/question/5c6818c4641b064a18a2575b Cơ hội rất hiếm! Hôm qua bạn Thiên An vừa nhận được 1 balo trị giá 350k đấy! Xem chi tiết :https://alfazi.edu.vn/question/5c6818c4641b064a18a2575b
ALFAZI THƯƠNG HIỆU HỌC TẬP SỐ 1 VN!
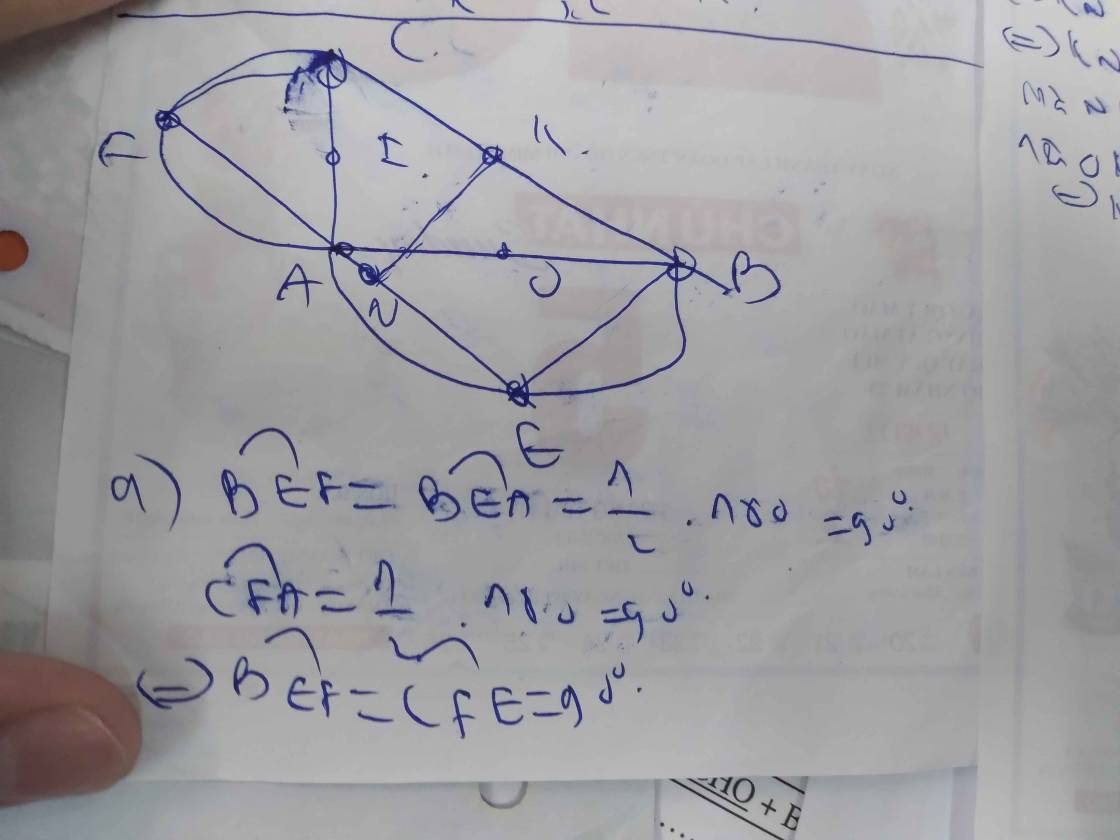
a) Ta thấy: Các góc ^AMB, ^ANC nội tiếp chắn nửa đường tròn => ^AMB = ^ANC = 900
=> BM và CN cùng vuông góc MN => BM // CN
Xét tứ giác BMNC: BM // CN, ^BMN = ^CNM = 900 => Tứ giác BMNC là hình thang vuông.
b) Gọi AK là trung tuyến từ đỉnh A của \(\Delta\)ABC. Dễ thấy IK là đường trung bình hình thang BMNC
=> IK // BM // CN. Mà BM,CN vuông góc MN nên IK vuông góc MN tại I => ^AIK = 900
=> I nằm trên đường tròn đường kính AK . Do AK cố định nên (AK) cố định
=> I chạy trên đường tròn (AK). Kết luận: ...