Giúp em bài 6 với 9 với ạ. Vẽ hình giúp en nx. Em cảm ơn ạ. 
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
HJ
1
Những câu hỏi liên quan
Vẽ hình và làm giúp em bài này với ạ, Em cảm ơn ạ
11 tháng 4 2023
a: góc CAO+góc CMO=180 độ
=>CAOM nội tiếp
b: Xét (O) có
CA,CM là tiếp tuyến
=>CA=CM và OC là phân giác của góc MOA(1)
Xét (O) co
DM,DB là tiếp tuyến
=>DM=DB và OD là phân giác của góc MOB(2)
CD=CM+MD=CA+DB
Từ (1), (2) suy ra góc COD=1/2*180=90 độ
c: AC*BD=CM*MD=OM^2=R^2
TN
0
HK
1
27 tháng 7 2023
a: góc AEB=góc ADB=90 độ
=>AEDB nội tiếp đường tròn đường kính AB
=>I là trung điểm của AB
b: Gọi H là giao của AD và BE
ABDE nội tiếp
=>góc HDE=góc HBA
=>góc HDE=góc HMN
=>DE//MN
26 tháng 10 2021
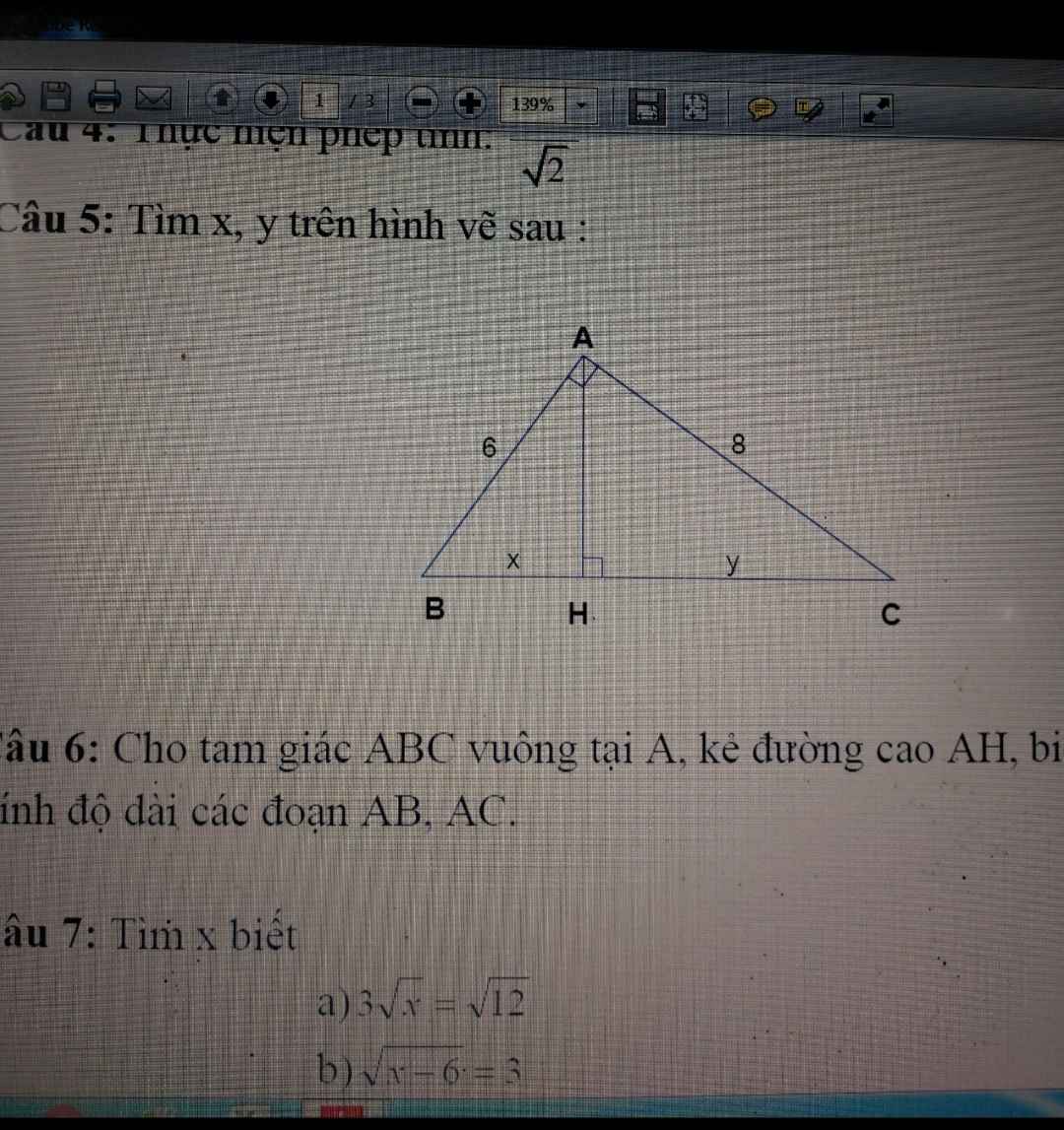
câu 5:
x=3,6
y=6,4
câu 6: chụp lại đề
câu 7:
a)ĐKXĐ: \(x\ge0\)
\(3\sqrt{x}=\sqrt{12}\\ \Rightarrow9x=12\\ \Rightarrow x=\dfrac{4}{3}\)
b) ĐKXĐ: \(x\ge6\)
\(\sqrt{x-6}=3\\ \Rightarrow x-6=9\\ \Rightarrow x=15\)
HN
2
26 tháng 8 2021
a: Xét ΔABD và ΔHBD có
BA=BH
\(\widehat{ABD}=\widehat{HBD}\)
BD chung
Do đó: ΔABD=ΔHBD
b: Ta có: ΔABD=ΔHBD
nên \(\widehat{BAD}=\widehat{BHD}\)
mà \(\widehat{BAD}=90^0\)
nên \(\widehat{BHD}=90^0\)
hay DH\(\perp\)BC
TN
1
26 tháng 10 2021
b: \(BC=\sqrt{89}\left(cm\right)\)
\(\sin\widehat{B}=\dfrac{5\sqrt{89}}{89}\)
\(\Leftrightarrow\widehat{B}\simeq32^0\)
\(\widehat{C}=58^0\)
H9
HT.Phong (9A5)
CTVHS
4 tháng 10 2023
Bài 6:
Ta có:
\(sin^2x+cos^2x=1\)
\(\Leftrightarrow cos^2x=1-sin^2x\)
\(\Leftrightarrow cos^2x=1-\left(\dfrac{1}{3}\right)^2=\dfrac{8}{9}\)
\(\Leftrightarrow cosx=\sqrt{\dfrac{8}{9}}=\dfrac{2\sqrt{2}}{3}\)
Mà: \(tanx=\dfrac{sinx}{cosx}\)
\(\Leftrightarrow tanx=\dfrac{1}{3}:\dfrac{2\sqrt{2}}{3}=\dfrac{1}{2\sqrt{2}}=\dfrac{\sqrt{2}}{4}\)
\(\Leftrightarrow\text{c}otx=\dfrac{1}{tanx}=1:\dfrac{\sqrt{2}}{4}=\dfrac{4}{\sqrt{2}}=2\sqrt{2}\)
Bài 10:
a: \(\overrightarrow{AB}+\overrightarrow{BO}+\overrightarrow{OA}\)
\(=\overrightarrow{AO}+\overrightarrow{OA}=\overrightarrow{0}\)
b: \(\overrightarrow{OA}+\overrightarrow{BC}+\overrightarrow{DO}+\overrightarrow{CD}\)
\(=\overrightarrow{OA}+\overrightarrow{DO}+\overrightarrow{BD}\)
\(=\overrightarrow{OA}+\overrightarrow{BO}=\overrightarrow{BA}\)