Trong mặt phẳng phức, tập hợp các điểm biểu diễn các số phức z thỏa mãn z.\(\overline{z}\)=1 là
A. một đường thẳng
B. một đường tròn
C. một elip
D. một điểm
Ai biết được tập hợp các điểm biểu diễn các số phức z thõa mãn trường hợp nào khác được các hình nào chỉ mình với! Xin cảm ơn !

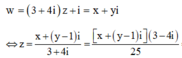
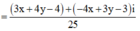
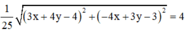
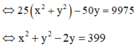
Đặt \(z=a+bi\Rightarrow\overline{z}=a-bi\)
Ta có \(z.\overline{z}=1\Leftrightarrow\left(a+bi\right)\left(a-bi\right)=1\)
\(\Leftrightarrow a^2-b^2i^2=1\Leftrightarrow a^2+b^2=1\)
\(\Rightarrow\) Tập hợp các số phức thỏa mãn điều kiện trên là một đường tròn có tâm là gốc tọa độ, bán kính 1 đơn vị độ dài