Tìm m để phương trình: x4 - (m+2)x2+m+1=0 có bốn nghiệm phân biệt.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
Nếu $m=-3$ thì PT trở thành: $7x^2-3=0$ có nghiệm $x=\pm \sqrt{\frac{3}{7}}$
-------------------------------------------------------------
Nếu $m\neq -3$Đặt $x^2=t$ thì pt trở thành:
$(m+3)t^2-(2m-1)t-3=0(*)$
1. Để pt ban đầu có 1 nghiệm thì PT $(*)$ có nghiệm $t=0$ và nếu có nghiệm còn lại thì nghiệm đó âm.
Để PT $(*)$ có nghiệm $t=0$ thì: $(m+3).0-(2m-1).0-3=0\Leftrightarrow -3=0$ (vô lý)
Do đó không tồn tại $m$ để pt có 1 nghiệm.
2. Để pt ban đầu có 2 nghiệm phân biệt thì PT $(*)$ có 1 nghiệm dương kép hoặc có 1 nghiệm dương và 1 nghiệm âm.
PT có 1 nghiệm dương, 1 nghiệm âm khi \(\left\{\begin{matrix} \Delta (*)=(2m-1)^2+12(m+3)> 0\\ P=\frac{-3}{m+3}<0\end{matrix}\right.\)
\(\Leftrightarrow m>-3\)
PT có nghiệm kép dương $\Leftrightarrow \Delta (*)=(2m-1)^2+12(m+3)=0\Leftrightarrow 4m^2+8m+37=0$ (vô lý)
Vậy $m>-3$
3.
PT ban đầu có 4 nghiệm phân biệt khi PT $(*)$ có 2 nghiệm dương phân biệt
Điều này xảy ra khi \(\left\{\begin{matrix} \Delta (*)=(2m-1)^2+12(m+3)>0\\ S=\frac{2m-1}{m+3}>0\\ P=\frac{-3}{m+3}>0\end{matrix}\right.\Leftrightarrow m< -3\)

Đặt \(x^2=t\left(t\ge0\right)\), phương trình trở thành:
\(t^2-2\left(m+1\right)t+2m+1=0\left(1\right)\)
Yêu cầu bài toán thỏa mãn khi phương trình \(\left(1\right)\) có hai nghiệm dương phân biệt
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta'=m^2>0\\t_1+t_2=2m+2>0\\t_1t_2=2m+1>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m>-\dfrac{1}{2}\\m\ne0\end{matrix}\right.\)

a)Thay m=-7 vào pt ta được: \(x^4+5x^2-14=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2=2\\x^2=-7\left(L\right)\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=\sqrt{2}\\x=-\sqrt{2}\end{matrix}\right.\)
Vậy...
b) Đặt \(t=x^2\left(t\ge0\right)\)
=>Với mỗi t dương ta tìm được hai nghiệm x phân biệt
Pttt: \(t^2-\left(m+2\right)t+3m+7=0\) (*)
Để pt ban đầu có hai nghiệm pb <=> pt (*) có 1 nghiệm dương duy nhất hoặc có hai nghiệm phân biệt trái dấu
TH1:PT (*) có 1 nghiệm dương duy nhất
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta=0\\-\dfrac{b}{2a}>0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m^2-8m-24=0\\\dfrac{m+2}{2}>0\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}m=4+2\sqrt{10}\\m=4-2\sqrt{10}\end{matrix}\right.\\m>-2\end{matrix}\right.\)\(\Rightarrow m=4+2\sqrt{10}\) (1)
TH2: Pt (*) có hai nghiệm phân biệt trái dấu
\(\Leftrightarrow ac< 0\) \(\Leftrightarrow3m+7< 0\) \(\Leftrightarrow m< -\dfrac{7}{3}\) (2)
Từ (1) (2) =>\(\left[{}\begin{matrix}m=4+2\sqrt{10}\\m< -\dfrac{7}{3}\end{matrix}\right.\)
trông kết quả em tự làm ra không được tròn nên em gửi câu hỏi lên đây. Hóa ra mình làm đúng (??????)


Phương trình (1) có hai nghiệm phân biệt khi phương trình (2) có nghiệm kép hoặc có 1 nghiệm dương và một nghiệm âm.
Phương trình (2) có một nghiệm số kép khi và chỉ khi Δ = 169 - 4m = 0
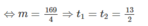
Phương trình (2) có một nghiệm số dương và một nghiệm số âm khi
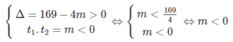
Vậy với m = 169/4 hoặc m < 0 thì phương trình (1) có 2 nghiệm phân biệt.

Chọn B.
Đặt t = x2, t ≥ 0.
Phương trình trở thành: t2 – 2(m + 1)t + 2m + 1 = 0 (2)
Phương trình (1) có bốn nghiệm phân biệt khi và chỉ khi PT (2) có hai nghiệm dương phân biệt t2 > t1 > 0.
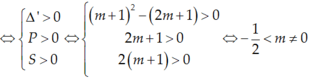
Khi đó PT(2) có bốn nghiệm là: ![]()
Bốn nghiệm này lập thành cấp số cộng khi :
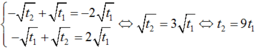
Theo định lý viet thì : 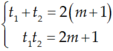
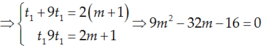
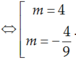
Vậy m = 4 hoặc 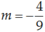 là những giá trị cần tìm.
là những giá trị cần tìm.

b) Đặt x 2 = t (t ≥ 0). Khi đó ta có phương trình: t 2 – mt – m – 1 = 0 (*)
Δ = m 2 - 4(-m - 1) = m 2 + 4m + 4 = m + 2 2
Phương trình đã cho có 4 nghiệm phân biệt khi và chỉ khi phương trình (*) có 2 nghiệm dương phân biệt
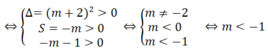


Phương trình (1) có ba nghiệm phân biệt khi phương trình (2) có 1 nghiệm số dương và 1 nghiệm bằng 0 khi:
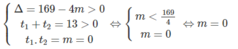


Phương trình (1) có 4 nghiệm phân biệt khi phương trình (2) có hai nghiệm số dương khi
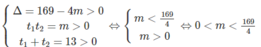

Đáp án D
Đặt t = x 2 ⇒ t ≥ 0. Phương trình đã cho trở thành t 2 − 2 t − m = 0 *
Để phương trình đã cho có 4 nghiệm phân biệt thì phương trình (*) có 2 nghiệm dương phân biệt
⇔ Δ ' = 1 + m > 0 S = 2 > 0 P = − m > 0 ⇔ − 1 < m < 0